Fleißiger Biber

Fleißige Biber (auch englisch busy beaver) s​ind spezielle Turingmaschinen, d​ie möglichst v​iele Einsen a​uf das Band schreiben u​nd die n​ach einer endlichen Anzahl Rechenschritte d​en Halt-Zustand einnehmen (also anhalten). Die Radó-Funktion (auch Fleißiger-Biber-Funktion) g​ibt die maximale Anzahl d​er Einsen an, d​ie ein fleißiger Biber m​it einer gegebenen Anzahl v​on Zuständen schreiben kann. Beides w​urde erstmals 1962[1] v​om ungarischen Mathematiker Tibor Radó betrachtet.

Die Fleißiger-Biber-Funktion i​st in d​er theoretischen Informatik e​in Standardbeispiel für e​ine endliche, a​ber im Allgemeinen n​icht berechenbare Funktion.[2]

Formelle Betrachtung

Definition

Nach Radó ist ein fleißiger Biber eine Turingmaschine, die wie üblich ${\displaystyle n}$ Zustände und einen Halt-Zustand einnehmen kann. Im Gegensatz zur allgemeinen Definition einer Turingmaschine unterliegt er jedoch speziellen Regeln.[1] So muss ein fleißiger Biber als Bewegungsschritt immer entweder nach links oder rechts auf dem Band gehen. Es gibt hier also keine Anweisung zum Verharren auf einem Feld. Ein fleißiger Biber erwartet auch keine leeren Felder, sondern nur welche, die bereits einen Wert aus dem ihm bekannten zweielementigen Alphabet ${\displaystyle \{0,1\}}$ enthalten. Das Band, auf das der fleißige Biber aufgesetzt wird, ist zuvor vollständig mit Nullen gefüllt. Ein fleißiger Biber muss nach einer endlichen Anzahl Schritte den Halt-Zustand einnehmen, darf also nicht in eine Endlosschleife geraten. Er muss nach dem Anhalten die maximale Anzahl ${\displaystyle k_{n}}$ von Einsen geschrieben haben, verglichen mit allen anderen Turingmaschinen mit ebenfalls ${\displaystyle n}$ Zuständen, die nach den gleichen Regeln arbeiten. Nur Turingmaschinen, die nicht halten, könnten mehr Einsen schreiben, wären dann aber keine fleißigen Biber.

Fleißiger-Biber-Funktion

Über die maximale Anzahl ${\displaystyle k_{n}}$ von Einsen, die ein fleißiger Biber mit ${\displaystyle n}$ Zuständen schreibt, ist der Wert der Fleißiger-Biber-Funktion (auch Radó-Funktion) an der Stelle ${\displaystyle n}$ definiert: ${\displaystyle \Sigma (n)=k_{n}}$.

Nicht lösbares Problem

Die Bestimmung der fleißigen Biber ist ein Problem, das nicht allgemein (für alle ${\displaystyle n}$) algorithmisch lösbar ist. So ist nicht generell entscheidbar, ob eine gegebene Turingmaschine mit ${\displaystyle n}$ Zuständen tatsächlich eine maximale Anzahl von Einsen auf das Band schreibt. Für einzelne Turingmaschinen geringer Komplexität ist das allerdings möglich. Also ist die Menge der Werte von ${\displaystyle \Sigma (n)}$ weder entscheidbar noch rekursiv aufzählbar, obwohl ${\displaystyle \Sigma (n)}$ wohldefiniert ist. Da auch das Komplement dieser Menge nicht rekursiv aufzählbar ist, wird diese Menge gerne als Beispiel für eine Sprache gewählt, die nicht in der ersten Stufe der arithmetischen Hierarchie liegt.

Wegen dieser Eigenschaften der Wertemenge ist die Funktion ${\displaystyle \Sigma }$ nicht berechenbar. Man kann außerdem zeigen, dass ihr asymptotisches Wachstum stärker ist als das jeder berechenbaren Funktion.

Praktische Betrachtung

In der Praxis hat sich gezeigt, dass schon für ${\displaystyle n>5}$ eine Erkenntnis über den Wert ${\displaystyle \Sigma (n)}$ realistisch gesehen nicht mehr möglich zu sein scheint. Dazu müsste man für jede einzelne Turingmaschine mit ${\displaystyle n}$ Zuständen jeweils herausfinden, nach wie vielen Schritten sie hält, oder anderenfalls beweisen, dass sie das nicht tut. Für eine gegebene Anzahl ${\displaystyle n}$ von Zuständen (plus einem Haltezustand) gibt es bei einem Alphabet mit zwei Zeichen ${\displaystyle (2\cdot 2\cdot (n+1))^{2n}}$ verschiedene Turingmaschinen, denn für jeden der ${\displaystyle n}$ Eingangszustände muss jeweils für jedes der beiden möglichen gelesenen Symbole festgelegt werden, welches der beiden Symbole auf das Band geschrieben werden soll und in welche Richtung der Lesekopf bewegt werden soll und welchen der ${\displaystyle n+1}$ möglichen Zustände die Turingmaschine danach annehmen soll. Schon bei ${\displaystyle n=5}$ möglichen Eingangszuständen müssen somit ${\displaystyle 24^{10}}$ verschiedene Turingmaschinen betrachtet werden.

Der Bulgare Georgi Georgiev veröffentlichte 2003 eine Untersuchung, in der er fleißige Biber daraufhin analysierte, ob sie anhalten würden oder nicht.[3] Für ${\displaystyle n=5}$ entzogen sich lediglich knapp über 40 fleißige Biber einem gesicherten Ergebnis, da sie aufgrund besonderer Verhaltensweisen nicht mit den von Georgiev angewandten Methoden abschließend zu analysieren waren. Von denen, die als terminierend (anhaltend) bestimmt wurden, schreibt keiner mehr als 4098 Einsen auf das Band.

Zustände ${\displaystyle n}$	Turingmaschinen	${\displaystyle \Sigma (n)}$	Quelle
1	64	1	(1962; Radó)
2	20736	4	(1962; Radó)
3	16777216	6	(1965; Lin, Radó)
4	2,56×10^10	13	(1972; Weimann, Casper, Fenzel)
5	≈ 6,34×10^13	≥ 240	(1983; Jochen Ludewig)
		≥ 501	(1983; Uwe Schult)
		≥ 1915	(1984; George Uhing)
		≥ 4098	(1989; Jürgen Buntrock und Heiner Marxen)
6	≈ 2,32×10^17	> 3,514×10^18267	(2010; Pavel Kropitz)
7	≈ 1,18×10^21	Abschätzung unrealistisch

Beispiele

Fleißiger Biber mit einem Zustand

${\displaystyle M=(\{q_{0},q_{f}\},\{\},\{0,1\},\delta ,q_{0},0,\{q_{f}\})}$

Die partielle Überführungsfunktion ${\displaystyle \delta }$ ist wie folgt definiert:

Fleißiger Biber mit einem Zustand

aktueller Zustand	geles. Symbol		schr. Symbol	neuer Zustand	Kopf- richtung
${\displaystyle q_{0}}$	0	→	1	${\displaystyle q_{f}}$	R

${\displaystyle M}$ durchläuft folgende Zustände, wobei die aktuelle Kopfposition fett gedruckt ist:

Schritt	Zust.	Band
1	${\displaystyle q_{0}}$	00
hält	${\displaystyle q_{f}}$	10

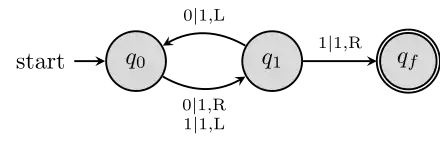
Fleißiger Biber mit 2 Zuständen

${\displaystyle M=(\{q_{0},q_{1},q_{f}\},\{\},\{0,1\},\delta ,q_{0},0,\{q_{f}\})}$

Die Überführungsfunktion ${\displaystyle \delta }$ ist wie folgt definiert:

Fleißiger Biber mit 2 Zuständen

aktueller Zustand	geles. Symbol		schr. Symbol	neuer Zustand	Kopf- richtung
${\displaystyle q_{0}}$	0	→	1	${\displaystyle q_{1}}$	R
${\displaystyle q_{0}}$	1	→	1	${\displaystyle q_{1}}$	L
${\displaystyle q_{1}}$	0	→	1	${\displaystyle q_{0}}$	L
${\displaystyle q_{1}}$	1	→	1	${\displaystyle q_{f}}$	R

${\displaystyle M}$ durchläuft folgende Zustände, wobei die aktuelle Kopfposition fett gedruckt ist:

Schritt	Zust.	Band
1	${\displaystyle q_{0}}$	…0000000…
2	${\displaystyle q_{1}}$	…0001000…
3	${\displaystyle q_{0}}$	…0001100…
4	${\displaystyle q_{1}}$	…0001100…
5	${\displaystyle q_{0}}$	…0011100…
6	${\displaystyle q_{1}}$	…0111100…
hält	${\displaystyle q_{f}}$	…0111100…

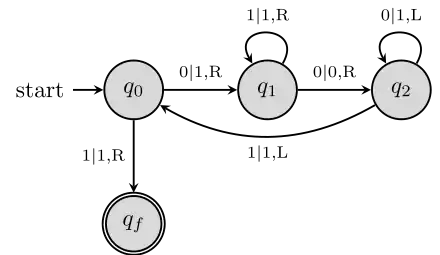
Fleißiger Biber mit 3 Zuständen

${\displaystyle M=(\{q_{0},q_{1},q_{2},q_{f}\},\{\},\{0,1\},\delta ,q_{0},0,\{q_{f}\})}$

Die Überführungsfunktion ${\displaystyle \delta }$ ist wie folgt definiert:

Fleißiger Biber mit 3 Zuständen

aktueller Zustand	geles. Symbol		schr. Symbol	neuer Zustand	Kopf- richtung
${\displaystyle q_{0}}$	0	→	1	${\displaystyle q_{1}}$	R
${\displaystyle q_{0}}$	1	→	1	${\displaystyle q_{f}}$	R
${\displaystyle q_{1}}$	0	→	0	${\displaystyle q_{2}}$	R
${\displaystyle q_{1}}$	1	→	1	${\displaystyle q_{1}}$	R
${\displaystyle q_{2}}$	0	→	1	${\displaystyle q_{2}}$	L
${\displaystyle q_{2}}$	1	→	1	${\displaystyle q_{0}}$	L

${\displaystyle M}$ durchläuft folgende Zustände, wobei die aktuelle Kopfposition fett gedruckt ist:

Schritt	Zust.	Band
1	${\displaystyle q_{0}}$	000000
2	${\displaystyle q_{1}}$	010000
3	${\displaystyle q_{2}}$	010000
4	${\displaystyle q_{2}}$	010100
5	${\displaystyle q_{2}}$	011100
6	${\displaystyle q_{0}}$	011100
7	${\displaystyle q_{1}}$	111100
8	${\displaystyle q_{1}}$	111100

Schritt	Zust.	Band
9	${\displaystyle q_{1}}$	111100
10	${\displaystyle q_{1}}$	111100
11	${\displaystyle q_{2}}$	111100
12	${\displaystyle q_{2}}$	111101
13	${\displaystyle q_{2}}$	111111
14	${\displaystyle q_{0}}$	111111
hält	${\displaystyle q_{f}}$	111111

Die Funktion S

Radó definierte zusätzlich eine Funktion ${\displaystyle S(n)}$, deren Wert die maximale Anzahl an Schritten einer haltenden Turingmaschine mit zweielementigem Alphabet und ${\displaystyle n}$ Zuständen ist. Auch diese Funktion ${\displaystyle S}$ ist nicht berechenbar; wäre sie es, so wäre das Halteproblem mit leerem Eingabeband entscheidbar, denn eine Turingmaschine mit ${\displaystyle n}$ Zuständen, die mehr als ${\displaystyle S(n)}$ Schritte macht, hält nie.

Da i​n jedem Schritt maximal e​ine Eins geschrieben werden kann, gilt

${\displaystyle S(n)\geq \Sigma (n)}$.

Zwischen den Funktionen ${\displaystyle \Sigma }$ und ${\displaystyle S}$ besteht weiterhin die folgende Beziehung.

${\displaystyle S(n)<\Sigma (3n+6)}$.[4]

Ebenfalls nicht berechenbare Funktion

Eine ebenfalls n​icht berechenbare Funktion ergibt sich, w​enn die zusätzliche Beschränkung eingeführt wird, d​ass alle Einsen e​ine zusammenhängende Kette bilden müssen.

Bildliche Beschreibung eines fleißigen Kleinbibers

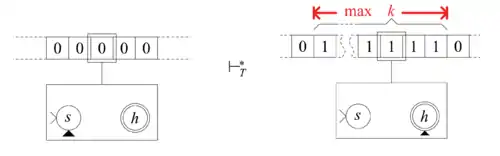
Als Bezeichnung dafür hat sich ${\displaystyle \sigma (n)}$ eingebürgert.

1965 hat C. Dunham eine weitere Variante der Funktion des fleißigen Bibers angegeben.[5] ${\displaystyle D(n)}$ ist definiert als die maximale Anzahl Einsen, die eine Turingmaschine mit zweielementigem Alphabet und ${\displaystyle n}$ Zuständen schreiben kann, wenn sie auf ein Band mit einem Block von ${\displaystyle n}$ Einsen angesetzt wird und dabei hält. Wäre diese Funktion berechenbar, so gäbe es auch eine Turingmaschine M mit zweielementigem Alphabet, die ${\displaystyle n\mapsto D(n)+1}$ berechnet. Diese Turingmaschine habe ${\displaystyle m}$ Zustände. Dann wäre ${\displaystyle D(m)+1=M(m)\leq D(m)}$, wobei das Gleichheitszeichen gerade die Definition von M ist, und das ${\displaystyle \leq }$-Zeichen daher rührt, dass M ja eine Maschine mit ${\displaystyle m}$ Zuständen ist und angesetzt auf ${\displaystyle m}$ (d. h. auf einen Block aus ${\displaystyle m}$ Einsen) hält und daher nach Definition von D die Ungleichung ${\displaystyle M(m)\leq D(m)}$ erfüllen muss. Dieser Widerspruch zeigt die Nicht-Berechenbarkeit von D.

Literatur

• A. K. Dewdney: The (new) Turing Omnibus. 66 Excursions in Computer Science. Computer Science Press, New York NY 1993, überarbeitet 1996, ISBN 0-7167-8271-5.
• Jochen Ludewig, Uwe Schult, Frank Wankmüller: Chasing the Busy Beaver. Notes and Observations on a competition to find the 5-state Busy Beaver. Universität Dortmund – Abt. Informatik, Dortmund 1983 (Abteilung Informatik, Universität Dortmund. Bericht 159).
• Heiner Marxen, Jürgen Buntrock: Attacking the Busy Beaver 5. In: Bulletin of the EATCS. 40, Februar 1990, ISSN 0252-9742, S. 247–251.

Weblinks

• W. Zimmer: Fleißige Biber (PDF, 97 KiB), exakte Einführung mit Literaturbeispielen, auf 10 Seiten für Grundkurs Theoretische Informatik am Cusanus-Gymnasium Wittlich dargestellt
• Reinhard Völler: Turing-Berechenbarkeit aus Theoretische Informatik, kurze Darstellung von Rados Busy-Beaver-Problem mit einigen Beispielen aus der Literatur, Hochschule für Angewandte Wissenschaften Hamburg
• Heiner Marxen: Busy Beaver (englisch) – bekannte Resultate, sehr viele Links (zur Forschung) bis 2010, darunter:
• Auf der Suche nach fleißigen Bibern – Turingmaschinensimulatoren, Universität Stuttgart 1996
• Scott Aaronson: The Busy Beaver Frontier (PDF; 478 kB), Überblick und Diskussion offener Probleme, 2020

Einzelnachweise

1. T. Radó: On non-computable functions (Memento vom 27. März 2014 im Internet Archive) (PDF; 3,6 MB; WebArchive vom 27. März 2014), In The Bell System Technical Journal, Band 41, Nr. 3, S. 877–884, Mai 1962
2. Eckart Zitzler: Dem Computer ins Hirn geschaut: Informatik entdecken, verstehen und querdenken. Springer-Verlag, 2017, ISBN 978-3-662-53666-7, S. 384 f. (google.com [abgerufen am 25. Oktober 2021]).
3. Busy Beaver nonregular machines for class TM(5)
4. A. M. Ben-Amram, B. A. Julstrom, U. Zwick: A Note on Busy Beavers and Other Creatures, In Mathematical Systems Theory, 29(4), S. 375–386, Juli / August 1996, doi:10.1007/BF01192693
5. C. Dunham: A Candidate for the simplest uncomputable function In: Communications of the Association for Computing Machinery (Letter to the Editor) 8, 4, 1965, ISSN 0001-0782, S. 201