Flächenmoment

Flächenmomente sind Querschnitts kennwerte: sie beschreiben, wie die Form der Querschnittsfläche die Eigenschaften länglicher Bauteile beeinflusst.

Querschnittsfläche

Anwendung finden die Flächenmomente bis 2. Grades (Flächenträgheitsmoment) insbesondere bei der Festigkeitsberechnung von Bauteilen und Strukturen. Flächenmomente ab dem 1. Grad sind auf eine bestimmte Ausrichtung des Querschnittes bezogen, sie haben demnach in verschiedenen Richtungen verschiedene Werte (d. h. je nachdem, auf welche Achse sie bezogen werden).

Flächenmomente n-ten Grades (allgemeine Definition)

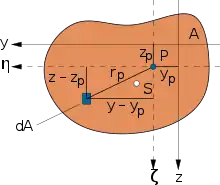
In den folgenden Kurzbeschreibungen liegt der Balken parallel zur x-Achse des Koordinatensystems und hat die Querschnittsfläche in der y-z-Ebene. Der Balken liegt symmetrisch im Koordinatensystem (genauer: die Hauptträgheitsachsen liegen parallel zu y- und z-Achse).

Das Flächenmoment n-ten Grades hat die folgende allgemeine Form:[1]

A_{i,j}=\int _{A}y^{i}\;z^{j}\;\mathrm {d} A

mit

n=i+j

Flächenmoment 0. Grades

Das Flächenmoment 0. Grades entspricht der Querschnittsfläche und hat die Einheit m²:

A=\int _{A}\mathrm {d} A

Flächenmoment 1. Grades

Die Flächenmomente 1. Grades werden auch als statisches Moment bezeichnet und haben die Einheit m³.

Bezogen auf die y-Achse:

S_{y}=\int _{A}z\;\mathrm {d} A

Bezogen auf die z-Achse:

S_{z}=\int _{A}y\;\mathrm {d} A

Aus diesen Momenten können (bei bekanntem Flächeninhalt $A$ ) die beiden Koordinaten des Schwerpunktes errechnet werden:

z_{s}={\frac {S_{y}}{A}};\quad y_{s}={\frac {S_{z}}{A}}

Flächenmoment 2. Grades

Die Flächenmomente 2. Grades sind auch unter dem Begriff Flächenträgheitsmoment bekannt und haben die Einheit [m⁴].

Sie geben den Einfluss der Form der Querschnittsfläche eines Balkens auf seine Steifheit an. Aus dem Flächenträgheitsmoment wird auch das Widerstandsmoment abgeleitet, welches den Einfluss der Form der Querschnittsfläche auf die Festigkeit beschreibt.

Flächenmoment 2. Grades bezogen auf die y-Achse:

I_{y}=\int _{A}z^{2}\;\mathrm {d} A

Flächenmoment 2. Grades bezogen auf die z-Achse:

I_{z}=\int _{A}y^{2}\;\mathrm {d} A

biaxiales Flächenträgheitsmoment:

I_{yz}=I_{zy}=-\int _{A}yz\ \mathrm {d} A

polares Flächenträgheitsmoment:

I_{P}=I_{y}+I_{z}=\int _{A}r^{2}\ \mathrm {d} A

Einzelnachweise

Jens Göttsche, Maritta Petersen: Festigkeitslehre - klipp und klar. Hanser Verlag, 2006, ISBN 978-3-446-40415-1 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Göttsche_Petersen-1] Jens Göttsche, Maritta Petersen: Festigkeitslehre - klipp und klar. Hanser Verlag, 2006, ISBN 978-3-446-40415-1 (eingeschränkte Vorschau in der Google-Buchsuche).