Fangstoß

Fangstoß ist ein Begriff aus dem Sportklettern und Bergsteigen und bezeichnet die maximale Kraft auf das Seil am Anseilpunkt bei einem Sturz des Kletterers. Der Kletterer spürt diese Kraft als Ruck, wenn der Fall vom Seil gestoppt wird. Die deutsche Fassung der einschlägigen Norm EN 892[1] verwendet den etwas präziseren Terminus Fangstoßkraft, in der Kletterliteratur ist jedoch die kürzere Bezeichnung Fangstoß verbreitet, die im Folgenden beibehalten wird.

Um den Fangstoß gering zu halten, besitzen Kletterseile eine sogenannte Sturzdehnung von bis zu 40 Prozent der eigenen Länge. Je weiter sich ein Seil dehnen kann, desto langsamer und weniger ruckartig kann die beim Sturz freiwerdende potentielle Energie des Kletterers auf das Seil übertragen werden und desto besser können die auf den Kletterer und die gesamte Sicherungskette wirkenden Kräfte reduziert werden. Alle Kletterseile müssen nach Euro-Norm 892 mindestens 5 Normstürze aushalten (d. h. Sturzzahl ≥ 5). Dennoch sollte aus Sicherheitsgründen ein Seil bereits nach einem harten Sturz aussortiert werden. Allerdings werden bei normalen Sportkletterstürzen nur Sturzfaktoren < 1 erreicht, die das Seil deutlich weniger schädigen als ein harter Sturz (Sturzfaktor > 1) oder gar ein Normsturz (Sturzfaktor ungefähr 1,7).

In einer Seilschaft zweier Kletterpartner ist auch der Gewichtsfaktor mitbestimmend für die Höhe des Fangstoßes. Ist der Sichernde bedeutend schwerer als der Kletternde, tritt bei ansonsten gleichen Sturzbedingungen ein höherer Fangstoß auf, der vom stürzenden Kletterer als härterer Sturz wahrgenommen wird. Ist der Sichernde hingegen bedeutend leichter als der Kletternde, wird der Sichernde im Sturzfall stärker in Richtung der ersten Zwischensicherung bzw. Seilumlenkung gezogen, was bei einem Anprallen gegen die Kletterwand zum reflexhaften Auslassen des Sicherungsseils und in der Folge zu einem Bodensturz des Kletterers führen kann. Der DAV empfiehlt zusätzliche Sicherungsmaßnahmen zu treffen, wenn der Kletternde mehr als 10 kg schwerer ist als der Sichernde. Vom bisher angegebenen Gewichtsfaktor wurde Abstand genommen.[2]

Normsturz

Der Fangstoß wird bei einem Normsturz gemessen und darf die durch EN bzw. UIAA-Norm festgelegten Werte nicht überschreiten:

Einfachseile im Einfachstrang: max. 12 kN
Halbseile im Einfachstrang: max. 8 kN
Zwillingsseile im Doppelstrang: max. 12 kN

In der Praxis ist der Fangstoß kleiner als bei einem UIAA Normsturz, da der Sturzfaktor kleiner als der Norm-Sturzfaktor ist, sobald das Seil durch mehrere Sicherungspunkte läuft. Dadurch ist die verfügbare Seillänge größer, das Seil kann mehr Energie aufnehmen und der Sturz wird bei gleicher Fallhöhe „weicher“. Gleichzeitig bewirkt die Reibung zwischen Seil und Sicherungspunkten, dass das Seil effektiv steifer wird, wodurch auch der Fangstoß wieder stärker wird. Diese beiden gegenläufigen Effekte lassen sich mathematisch beschreiben[3].

Physikalische Betrachtungen

Der Fangstoß für ein dynamisches Kletterseil kann für das gängige HO Seilmodell näherungsweise leicht berechnet werden. Darin wird die Kraft auf das Seil mit dem Hookeschen Gesetz angenähert. Dieses beschreibt das elastische Verhalten von Festkörpern, deren elastische Verformung $\varepsilon$ linear proportional zur anliegenden Spannung $\sigma$ ist. Die Proportionalitätskonstante ist der Elastizitätsmodul E, eine Materialkonstante, die unabhängig von der Seillänge und dem Seilquerschnitt ist.

Fangstoß in Abhängigkeit vom Sturzfaktor mit E·q = 33.3 [kN]

E={\frac {\rm {Spannung}}{\rm {Dehnung}}}={\frac {\sigma }{\varepsilon }}={\frac {F/q}{x/l}}

F: Kraft, q: Querschnittsfläche, x: Ausdehnung (= Δl Längenänderung), l: Länge des Seils.
Daraus folgt der bekannte Zusammenhang zwischen Kraft und Dehnung.

F={\frac {E\cdot q}{l}}\,x

Dabei ist E·q/l = D die übliche Federkonstante, die von der Länge l abhängt.

Um die Energie zu berechnen, die bei der Dehnung x im Seil steckt, muss man die Kraft nach dem Weg von 0 bis x integrieren.

{\rm {{Energie}=\int _{0}^{x}{F\,dx}={\frac {E\cdot q}{2\,l}}\,x^{2}}}

Für die maximale Seildehnung x_max nach einer Sturzhöhe h setzt man die potentielle Energie mg (h+x_max) gleich der Dehnungsenergie. Beim unteren Umkehrpunkt ist die gesamte potentielle Energie in Dehnungsenergie übergegangen.

{\frac {E\cdot q}{2\,l}}\,x_{\rm {max}}^{2}=mg\,(h+x_{\rm {max}})

Auflösen nach der maximalen Seildehnung x_max ergibt:

x_{\rm {max}}={\frac {mg\,l}{E\cdot q}}+{\sqrt {\left({\frac {mg\,l}{E\cdot q}}\right)^{2}+{\frac {2\,mg\,lh}{E\cdot q}}}}

Für den Fangstoß F_max = (E·q/l) x_max ergibt sich dann nach Einsetzen von x_max:

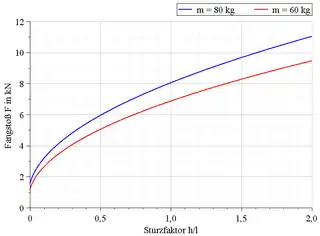
F_{\rm {max}}=mg+{\sqrt {(mg)^{2}+2\,mg\,E\cdot q{\frac {h}{l}}}}

Der Fangstoß hängt also vom Sturzfaktor f = h/l, sowie von der Materialkonstante E, dem Seilquerschnitt q und dem Gewicht des Kletterers ab. Typische experimentelle Werte für E·q von Einfachseilen liegen in einem Bereich von 30 bis 50 [kN]. Je mehr Seil ausgegeben ist, desto weicher wird das Seil, was die höhere Fallenergie gerade kompensiert. Die maximale Kraft auf den Kletterer ist F_max reduziert um das Gewicht des Kletterers mg.

Bei einem Nachstiegssturz ohne Schlappseil, also Sturzfaktor h/l = 0, erhält man als Fangstoß F_max = 2 mg; d. h. eine Belastung mit doppeltem Körpergewicht.

Dieses einfache ungedämpfte HO-Modell eines Kletterseils kann jedoch das Verhalten realer Seile für den gesamten Sturzprozess nur unzureichend beschreiben. Dieser kann erklärt werden, wenn der ungedämpfte HO bis zum Fangstoß durch einen nichtlinearen Term ergänzt wird, und dann, nahe der maximalen Kraft im Seil, eine innere Reibung im Seil hinzugefügt wird, die für die schnelle Relaxation des Seils in seine Ruheposition sorgt.[4][5]

Sobald das Seil durch mehrere Karabiner läuft, muss eine zusätzliche Reibungsart berücksichtigt werden, die so genannte trockene Reibung zwischen Seil und den Karabinern. Dem letzten geklippten Karabiner kommt bei einem Sturz ein besonderes Gewicht zu, da der Umlenkwinkel für das Seil maximal, d. h. 180° wird. Trockene Reibung führt zu einer effektiven Seillänge, die kleiner ist als die "ausgegebene Seillänge" (das ist die Seillänge zwischen dem Kletternden und Sichernden in ungedehntem Zustand), wodurch der Fangstoß vergrößert wird. Trockene Reibung ist auch für den Seilzug verantwortlich, der immer dann auftritt, wenn das Seil über Felsunebenheiten läuft oder durch mehrere Sicherungspunkte, die nicht auf einer Linie liegen. Dieser Seilzug kann durch ein effektives Gewicht des Seils beschrieben werden, das immer größer gleich dem eigentlichen Seilgewicht ist. Es hängt exponentiell von der Summe der Winkel ab, die beim Einhängen in die Sicherungspunkte entstehen[3].

Siehe auch

Einzelnachweise

DIN EN 892:2012-11, Bergsteigerausrüstung - Dynamische Bergseile - Sicherheitstechnische Anforderungen und Prüfverfahren; Deutsche Fassung EN 892:2012
Deutscher Alpenverein: Sportklettern: Sichern mit Gewichtsunterschied. 2017, abgerufen am 7. Februar 2018 (deu).
Leuthäusser, Ulrich: Physics of climbing ropes: fall factors, impact forces and rope drag. (pdf; 195 kB) 2011, abgerufen am 18. Januar 2011 (eng).
Leuthäusser, Ulrich: The physics of a climbing rope under a heavy dynamic load. In: Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology. doi:10.1177/1754337116651184
Physik eines Kletterseils. 2015, abgerufen am 28. Juni 2016.

Literatur

Pit Schubert, Pepi Stückl: Alpin-Lehrplan, Bd. 5 (Sicherheit am Berg, Ausrüstung, Sicherung). München: BLV, 2003. ISBN 3-405-16632-2

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] DIN EN 892:2012-11, Bergsteigerausrüstung - Dynamische Bergseile - Sicherheitstechnische Anforderungen und Prüfverfahren; Deutsche Fassung EN 892:2012

[2] Deutscher Alpenverein: Sportklettern: Sichern mit Gewichtsunterschied. 2017, abgerufen am 7. Februar 2018 (deu).

[uleuthaeusser-3] Leuthäusser, Ulrich: Physics of climbing ropes: fall factors, impact forces and rope drag. (pdf; 195 kB) 2011, abgerufen am 18. Januar 2011 (eng).

[leuthaeusser-4] Leuthäusser, Ulrich: The physics of a climbing rope under a heavy dynamic load. In: Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology. doi:10.1177/1754337116651184

[5] Physik eines Kletterseils. 2015, abgerufen am 28. Juni 2016.