Ernst Barthel
Ernst Philipp Barthel (* 17. Oktober 1890 in Schiltigheim; † 16. Februar 1953 in Oberkirch (Baden)) war ein elsässischer Philosoph, Mathematiker und Erfinder.[1] In den 1920er und 1930er Jahren lehrte er als Privatdozent für Philosophie an der Universität Köln. Ab 1924 war Barthel Herausgeber der Zeitschrift Antäus. Blätter für neues Wirklichkeitsdenken, welche als Organ der von ihm in Köln gegründeten Gesellschaft für Lebensphilosophie fungierte. Barthel pflegte philosophische Freundschaften mit seinen Landsleuten Albert Schweitzer und Friedrich Lienhard.

Leben
Ernst Barthel wurde 1890 als Sohn von Philipp Barthel und dessen Ehefrau Salomea Barthel geborene Schaeffer geboren. Barthel begann nach einem hervorragenden Abitur im Jahr 1909 entgegen der Erwartung seiner Lehrer[2] ein Studium der Philosophie an der Universität Straßburg, das er 1913 mit dem Doktortitel abschloss.[3] Nach dem Ersten Weltkrieg ging er an die Universität Köln, wo er sich 1921 habilitierte.[4] Hier blieb seine Karriere aufgrund universitärer Intrigen zunächst in der prekären Stellung eines Privatdozenten stecken. Den Nationalsozialisten war er der Frankophilie verdächtig, was die Erlangung einer festen Anstellung weiter verhinderte. Trotz zaghafter Versuche, sich mit dem Regime zu arrangieren, wurde er im November 1940 vom Reichserziehungsminister Bernhard Rust ohne ersichtlichen Grund aus der Universität entlassen.[5] Vermutlich spielten religiös-metaphysische Äußerungen in seinem Buch Der Mensch und die ewigen Hintergründe, vor allem aber die angebliche Nähe des Autors der elsässischen Geistesschicksale (1928) zu Frankreich[6] hierbei eine Rolle. Ernst Barthel war Mitglied im NSLB.[7]
Nach dem Zweiten Weltkrieg war ihm die Rückkehr ins Elsass verwehrt, weil man ihm in Frankreich seine Übersiedlung nach Deutschland nach dem Ersten Weltkrieg ankreidete. Er ließ sich auf der anderen Rheinseite in Deutschland nieder und starb 1953 im badischen Oberkirch.
Der Nachlass Barthels liegt in der Stadt- und Universitätsbibliothek in Frankfurt am Main.
Philosophie
Das Grundprinzip von Barthels Philosophie ist die Polarität, die er als fundamental gestaltendes Gesetz in allem Existierenden begriff. Sein philosophisches Programm zielt bereits mit seiner Dissertation[8] darauf ab, eine erkenntnistheoretisch einwandfreie Metaphysik mit Nähe zum christlichen Platonismus zu schaffen. Als geistige Ausgangspunkt nennt er selbst Arthur Schopenhauer und vor allem Immanuel Kant: "Denn neben Schopenhauer ist niemand, dem wir eine so nachhaltige Beeinflussung und dauerhafte Lehre zu verdanken hätten als Kant."[9] Außerdem bezieht sich Barthel immer wieder auf die naturwissenschaftlichen Arbeiten J.W. v. Goethes.
Als zentralen Bestandteil seiner philosophischen Arbeit entwickelte er eine eigenständige Geometrie (Polargeometrie), einer sphärischen Geometrie auf Grundlage Riemannscher bzw. elliptischer Axiomatik.
Grundüberlegungen
Philosophie, Geometrie und Kosmologie sind im Denken Barthels unmittelbar aufeinander bezogen. Am naturwissenschaftlichen Weltbild, das er als "Pseudo-Kantianismus" bezeichnete,[10] kritisierte er folglich dessen reduktionistische Orientierung sowie die mangelnde ethische und menschbezogene Dimension. Besonders auch auf das kopernikanische Weltbild bezogen betonte er mehrfach: "Ich kann mich nicht damit abfinden, die Welt und die ganze Menschheit auf ein winziges, im unendlichen Raum verlorenes Staubkorn reduziert zu sehen."[11]
So entwarf er auch seine Polargeometrie als Gegenentwurf zur naturwissenschaftlichen Kosmologie[12]. In seiner polargeometrischen Kosmologie rückte er die Erde ins Zentrum des Universums, die dieses auch zum Großteil ausfüllte und damit keinen Platz mehr für unendliche Entfernungen bot: "Geometrie wird erst voll und ganz exakte Wissenschaft, wenn die Endlosigkeitsnebel, die man bisher noch an ihrem Horizont bemerkte, bis auf den letzten Rest vertrieben werden."[13]
Damit trat Barthel gegen den Vorrang der Naturwissenschaften vor der Philosophie an. In einer frühen Schrift formuliert er seinen Anspruch kämpferisch: "Die Philosophie hat lange genug nach der Pfeife der Naturwissenschaft getanzt."[14]
Auf ähnliche Weise misstraute er der Evolutionstheorie und suchte einen Mittelweg zwischen Evolutionismus und Kreationismus.[15] Fernand Criqui hält die Berücksichtigung der menschlichen Ethik für den Dreh- und Angelpunkt in Barthels Philosophie, die im Werk Barthels jedenfalls den Vorrang vor „naturwissenschaftlicher Wahrheit“ gehabt habe.[16] Entsprechend sah Barthel den Widerstand der etablierten Wissenschaft gegen seine Polargeometrie und von der zeitgenössischen Astronomie abweichenden kosmologischen Thesen überhaupt dadurch begründet, "weil die Weltherrschaft allzufrühen Irrtums und egoistischer Gewalt in Gefahr steht, durch die gerechten Gottesgesetze der Polarität (organischen Zweiheit) ihrer Macht verlustig zu gehen."[17]
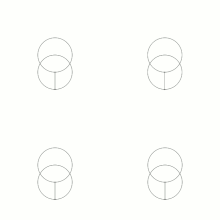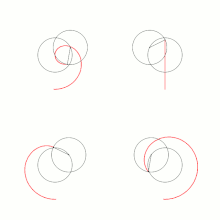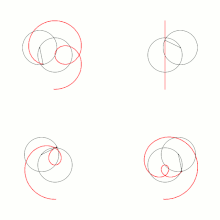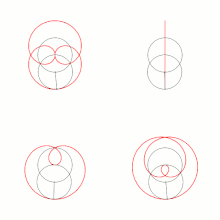
Barthel bezieht sich in seinem Werk systematisch auf zwei Prinzipien, deren Grundlage er aus der Struktur des menschlichen Bewusstseins ableitet.[18] Das erste Prinzip sei der polare Gegensatz des endlichen Bewusstseins zwischen konkreter Existenz und absoluten Kategorien (z. B. Wille/Vorstellung, praktisch/wissenschaftlich, quantitativ/qualitativ, beziehungsvoll/unmittelbar[19] etc.), den er als Voraussetzung aller Welterkenntnis sah und der daher auch in der Vorstellung des Kosmos verwirklicht sein müsse.[20] Als organische Manifestation des Prinzips versteht Barthel die Verkopplung von Kreisbewegungen, die er als grundlegendes Konstruktionsprinzip der Natur vorschlägt. Zu dessen Verdeutlichung entwickelt Barthel seinen sog. Transformationszirkel.[21] Der Transformationszirkel erzeugt Kurven, die genau die Mitte zwischen Epi- und Hypotrochoiden bilden. Damit stellt der Zeichenapparat einen wissenschaftlichen Vorläufer des in den 1960er Jahren erfundenen Spirographen dar.
Die polare Verkopplung von Kreisbewegungen verwendet Barthel z. B. konkret als formale Grundlage seiner Farbtheorie[22] sowie zur Beschreibung natürlicher Formen wie z. B. denen der Diatomeen.[23]
Das Wesen der Polargeometrie
Barthel legt ausführlich dar, warum seiner Meinung nach von allen axiomatisch formulierbaren Geometrien lediglich der Geometrie nach Riemann’scher Axiomatik ein objektives Recht zukomme. Da er die „Unendlichkeit“ kategorisch ablehnt, müssten in den übrigen Geometrien durch die Notwendigkeit unendlich weit entfernter bzw. verschwindender Punkte „Wunder“ geschehen, die aus erkenntnistheoretischer Sicht als „Traumbestandteile“ zu überwinden seien.[24] Diese Überwindung leistet seiner Einschätzung nach die Polargeometrie.
Der geometrische Raum der Polargeometrie ist durch zwei wesentliche Eigenschaften gekennzeichnet:
- Der Gesamtraum verfügt über einen maximalen, endlichen Durchmesser, die Raumkonstante,
- Jeder vollständige Schnitt durch den Gesamtraum lässt sich topologisch als Kugel veranschaulichen, d. h. als eine Ebene, die makroskopisch in sich selbst zurückläuft.
Damit werden Geraden zu Objekten mit den Eigenschaften von Großkreisen, und das mathematische Formelwerk zur Berechnung von makroskopischen Entfernungen und Flächen das der sphärischen Geometrie.
Ende der 1930er Jahre veröffentlichte Barthel außerdem noch einige Schriften, in denen er behauptet, dass in einigen Lehrsätzen der euklidischen Geometrie konkrete Ungenauigkeiten bestünden. Unter anderem glaubte er, dass der Wert der Zahl Pi für Kreisumfang und Kreisfläche um etwa 1/270 voneinander abwichen.[25]
Kosmogonie nach der Polargeometrie
Auf Basis der Überzeugung, dass die sphärische Geometrie Riemannscher Axiomatik die realen Raumverhältnisse des Kosmos beschreibt, entwickelte Barthel eine sphärische Kosmologie. Dabei betont er, dass er die kopernikanische "Planetenmathematik" unverändert belässt und nur die zugrunde liegende Geometrie überarbeitete.

Sein revolutionärste Idee dabei ist, die Erde als kosmisch groß aufzufassen, d. h. als Totalebene, Maximalkugel oder Äquatorebene eines sphärischen und damit zyklischen Raums. Die Topologie einer solchen (Total-)Ebene ist abbildbar auf eine Kugeloberfläche, so dass die Ebene selbst und alle Geraden auf ihr in sich selbst zurücklaufen. Das Gleiche gilt polargeometrisch ebenfalls für jede beliebige Gerade oder Ebene im Kosmos.
Messtechnisch sei die Erdoberfläche der Totalerde jedoch absolut eben und ohne jede Krümmung nach oben oder unten. Die offenkundige Schwierigkeit, etwas in sich selbst Zurücklaufendes zugleich als Ungekrümmtes zu denken, sei ein "Punkt, den man nicht beurteilen darf, ohne ihn ganz und gar begriffen zu haben", denn in ihm liege eine wesentliche Synthese "zwischen Euklidischer Solidität des Denkens und Riemannschem Ganzheitsaxiom".[26]
Entscheidend für die Einordnung dieser Auffassung ist es zu bemerken, dass dieser vermeintliche Widerspruch eine Entsprechung zur bis heute bestehenden Schwierigkeit bei der Beschreibung eines unbegrenzten, aber nicht unendlichen Universums besitzt.
Zur Beschreibung der Planetenbahnen ersetzte Barthel die kopernikanische Translationsbewegung der Erde durch eine kugelgeometrische Drehbewegung, die als jährliche Rotation der täglichen überlagert sei. Fixsterne sind nach Barthel außerdem keine Folge leuchtender Materie, sondern Individuationspunkte des Sonnenlichts, das am kosmischen "Raumkristall" gebeugt wird.
Folgerungen der Barthelschen Kosmogonie sind u. a., dass Licht sich nicht geradlinig ausbreite, sondern gravitativ beeinflusst werde und dass die Erdbeschleunigung g nicht konstant sei, sondern das Gewicht vom oberen Himmelspol (Null) zum unteren Erdpol (maximal) hin zunehme.[27]
Unter Annahme seines Maximalkugel-Umfanges als Erdumfang folgert Barthel, dass die Ausmaße und Entfernungen der Himmelskörper wesentlich geringer sein müssten, als die euklidische Geometrie sie berechnete. Barthel hielt auf Grundlage seine sphärischen Parallelenaxioms Mondkrater von 200 km Durchmesser und Mondberge von 8000 m Höhe für "groteske Dinge". Er berechnete stattdessen für die Mondoberfläche maximale Erhebungen von 40 m und Schluchten von 1,5 bis 2,5 km Länge sowie einen Abstand des Mondes von der Erde von nur 2000 km – anstatt der euklidisch-kopernikanischen Entfernung von knapp 400 000 km,[28] von der die Astronomie bis heute ausgeht.
Barthel hingegen ging noch bis zu seinem Tode 1953 davon aus, dass sich seine Theorie durch den Fortschritt der Luft- und Raumfahrt bestätigen würde: "Für mein System wird jeder Stratosphärenflug zum Pionier der Idee, denn je mehr man den Raum über der Erdfläche konkret erkundet, um so mehr muß man darauf stoßen, daß die Inflationszahlen nicht zutreffen."[29]
Rezeption
Während Barthels konventionell philosophische Arbeiten bis heute zitiert werden[30], sind seine geometrisch-kosmologischen Arbeiten weitgehend vergessen und werden, wenn überhaupt, als kuriose Randnotiz behandelt.
Wenn auch manche seiner Kollegen seine Theorie für geometrisch möglich und logisch konsistent gehalten haben sollen, lehnte die überwiegende Mehrheit seiner Zeitgenossen sie vehement ab. Manche griffen zu Lebzeiten Barthels auch zum Mittel des „Pesthauchs der persönlichen Verleumdung“[31], indem sie spotteten, er „lehre, die Erde sei eine Scheibe“ oder ihn unumwunden für verrückt erklärten, wodurch seine Karriere zugrundegerichtet wurde.[32]
Barthel betrachtete seine Theorie selbst als vollauf bestätigt und bezeichnete sie sogar als den "bedeutsamsten Gedanken des Jahrhunderts", wie er in seiner Autobiographie schrieb.[33] Laut Barthel soll auch der in Konstanz tätige Astronom Leonid Andrenko Barthels Hauptgedanken als „zu den genialsten gehörend, die jemals vorgeschlagen wurden“ erachtet haben und dafür eingetreten sein, „dass man davon Kenntnis nehme und darüber nachdenke“.[34]
Durch die Raumfahrt nach dem Zweiten Weltkrieg mit ihren Entfernungsmessungen, Satellitenfotos, die die Erde als Kugel darstellen und schließlich direkte Landungen auf Mond und Mars wurden allerdings immer mehr Belege erbracht, die die konkreten Folgerungen Barthels als falsch erwiesen,[35] auch wenn die objektiv im physikalischen Universum vorliegende Geometrie bis heute eine offene Frage ist.[36]
Werke (Auswahl)
- Elemente der transzendentalen Logik, Dissertation, Straßburg, 1913
- Die Erde als Totalebene. Hyperbolische Raumtheorie mit einer Voruntersuchung über die Kegelschnitte, 1914
- Vertikaldimension und Weltraum. Neue Beweise gegen die Kugelgestalt der Erde, 1914
- Der Irrtum «g». Ein Traktat über den freien Fall, 1914
- Harmonische Astronomie, 1916
- Polargeometrie, 1919
- Goethes Wissenschaftslehre in ihrer modernen Tragweite, 1922
- Goethes Relativitätstheorie der Farbe. Nebst einer musikästhetischen Parallele, 1923
- Lebensphilosophie, 1923
- Philosophie des Eros, 1926
- Deutschlands und Europas Schicksalsfrage, in: Zeitschrift für Geopolitik, 3, 1926, S. 303–309.
- Form und Seele. Dichtungen, 1927
- Die Welt als Spannung und Rhythmus, 1928 (Digitalisat).
- Albert Schweitzer as Theologian, in: The Hibbert Journal, XXVI, 4 (1928)
- Elsässische Geistesschicksale. Ein Beitrag zur europäischen Verständigung. Carl Winter, Heidelberg 1928, Alsatia Verlag, Guebwiller 1928
- Erweiterung raumtheoretischer Denkmöglichkeiten durch die Riemannsche Geometrie, in: Astronomische Nachrichten, Vol. 236 (1929), pp. 139–148.
- Goethe, das Sinnbild deutscher Kultur, 1930
- Die Monadologie der beiden Welten. Abriß der Metaphysik, Jahrbuch der Elsaß-Lothringischen Wissenschaftlichen Gesellschaft zu Straßburg, 3. 1930, S. 147–185
- Kosmologische Briefe. Eine neue Lehre vom Weltall, 1931
- Vorstellung und Denken. Eine Kritik des pragmatischen Verstandes. 1931
- Einführung in die Polargeometrie, 2. wesentlich verb., erg. und umgearb. Auflage der „Polargeometrie“, 1932
- Beiträge zur transzendentalen Logik auf polaristischer Grundlage. 1932
- Geometrie und Kosmos, 1939
- Die Kosmologie der Großerde im Totalraum. Hillmann, Leipzig 1939
- Der Mensch und die ewigen Hintergründe. 1939. Dieses Buch "wurde vom Nationalsozialismus für jede kommende Auflage verboten", Barthel, Mein Opfergang S. 230.
- Die Erde als Grundkörper der Welt. Ebertin, Erfurt 1940. Laut Barthels Autobiographie, S. 231, wurde diese Schrift 1941 von der Gestapo eingestampft.
- Friedrich Lienhard, die Künstlerseele aus dem deutschen Elsaß. Alsatia, Kolmar 1941
- Nietzsche als Verführer. 1947
- Mein Opfergang durch diese Zeit. Ein Leben im Kampf um Wahrheit und ein elsässisches Geistesschicksal. Hrsg. Georg Duve. Monsenstein und Vannerdat, Münster 2005
Literatur
- Jean-Paul Wurtz: Ernst Barthel: philosophe alsacien (1890 – 1953). Recueil d'études publié à l'occasion du centenaire de sa naissance. Presses Univ. de Strasbourg, 1991
- Jean-Paul Sorg: Ernst Barthel ou la tentation gnostique de la philosophie. S. 19–36
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 47–76
- Fernand Criqui: Ein tragisches Elsässerschicksal: Ernest Barthel, in: Der grosse Straßburger Hinkende Bote, 1954, S. 110–112
Weblinks
- Werke von oder über Ernst Barthel im WorldCat Katalog
- Interaktive Simulation des Barthel`schen Transformationszirkels (in Unity3D und alternativ in html5)
Einzelnachweise
- cf. VDI-Nachrichten, 19. April 1933, Beschreibung des Patents zu Ernst Barthels Transformationszirkel
- Ernst Barthel: Mein Opfergang durch diese Zeit, Hrsg.: Georg Duve, Verlag MV Wissenschaft, 2005 (posthum), S. 55
- Fernand Criqui: La vie et l'œuvre de Barthel. In: Jean-Paul Wurtz: Ernst Barthel: philosophe alsacien (1890 - 1953). Recueil d'études publié à l'occasion du centenaire de sa naissance. Presses Univ. de Strasbourg, 1991, S. 19–36
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 56
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 60 f.
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 61
- Ideologische Mächte im deutschen Faschismus Band 5: Heidegger im Kontext: Gesamtüberblick zum NS-Engagement der Universitätsphilosophen, George Leaman, Rainer Alisch, Thomas Laugstien, Verlag: Argument Hamburg, 1993, ISBN 3886192059
- Ernst Barthel: Elemente der transzendentalen Logik. Dissertation, Straßburg, 1913.
- Ernst Barthel: Beiträge zur transzendentalen Logik auf polaristischer Grundlage, Universitätsverlag R. Noske, Leipzig, S. 7
- Ernst Barthel: Vorstellung und Denken. Eine Kritik des pragmatischen Verstands, Verlag Ernst Reinhard, 1931, passim
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 52, dort auf französisch zitiert: Je ne puis me résigner à voir notre monde et toute l'humanité réduits à une infime particule de poussière perdue dans l'espace infini. – Vgl. auch Ernst Barthel: Polargeometrie S. 47 f.
- Jean-Paul Sorg: Ernst Barthel ou la tentation gnostique de la philosophie. In: Jean-Paul Wurtz: Ernst Barthel: philosophe alsacien (1890-1953). Recueil d'études publié à l'occasion du centenaire de sa naissance. Presses Univ. de Strasbourg, 1991, S. 26
- Ernst Barthel: Polargeometrie. 1918.
- Ernst Barthel: Der Irrtum "g". Ein Traktat über den freien Fall. Leipzig, Hillmann 1914, S. 6.
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 56-58
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 58
- Ernst Barthel, Die Kosmologie der Großerde im Totalraum. Hillmann, Leipzig 1939, S. 5
- Ernst Barthel: Elemente der transzendentalen Logik, Universitätsverlag R. Noske, Leipzig, 1932, S. 26f
- Ernst Barthel: Elemente der transzendentalen Logik, Universitätsverlag R. Noske, Leipzig, 1932, S. 61
- Barthel, Kosmologie der Großerde, S. 28
- cf. VDI-Nachrichten, 19. April 1933
- Komplementaristische Wellenmechanik. Eine Rechtfertigung der Goethe'schen Farbenlehre., Jahrbuch der Elsaß-Lothringischen Wissenschaftlichen Gesellschaft zu Straßburg, 1938, S. 240–251
- Mensch und Erde im Kosmos, Verlag für Volkskunst und Volksbildung, 1939, S. 58–82
- Ernst Barthel: Einführung in die Polargeometrie, Verlag Robert Noske, Leipzig, 1932, S. 5 f. und S. 90
- Ernst Barthel: Geometrie und Kosmos ohne Maßlosigkeit und ohne Unterschlagung kleiner Differenzen, Verlag Otto Hillmann, 1939, S. 10f
- E. Barthel, Vorstellung und Denken, Verlag Ernst Reinhard, 1931, S. 181
- Ernst Barthel: Der Irrtum "g". Ein Traktat über den freien Fall. Leipzig, Hillmann 1914, v. a. S. 35. – Ernst Barthel: Kosmologie der Großerde im Totalraum S. 12 f.
- E. Barthel, Die Kosmologie der Großerde im Totalraum. Leipzig 1939, S. 11
- E. Barthel, Die Kosmologie der Großerde im Totalraum., S. 11
- z. B. Hans Otto Seitschek: Religionsphilosophie als Perspektive - eine neue Deutung von Wirklichkeit und Wahrheit, 2017, S. 154
- Fernand Criqui: Ein tragisches Elsaesserschicksal: Ernst Barthel, 1954
- Ernst Barthel: Mein Opfergang durch diese Zeit, passim
- Ernst Barthel: Mein Opfergang durch diese Zeit, S. 119.
- Ernst Barthel: Mein Opfergang durch diese Zeit, S. 184.
- Fernand Criqui: La vie et l'œuvre de Barthel. S. 54
- A. Filler: Euklidische und Nicht-euklidische Geometrie, S. 231