Elastizitätsdiagramm
Ein Elastizitätsdiagramm ist eine grafische Abbildung, die den zeitlichen Verlauf zweier ökonomischer Größen in Relation zueinander setzt. Daraus lassen sich Rückschlüsse über einen Ursache-Wirkungszusammenhang ableiten. Das Elastizitätsdiagramm wird gebildet aus einem Punktdiagramm (Streuungsdiagramm, XY-Diagramm) mit der Besonderheit, dass die einzelnen Datenpunkte in zeitlicher Reihenfolge miteinander verbunden werden. Die entstehenden Linienverläufe können typische Muster aufweisen, mit denen bestimmte dynamische Reaktionsmuster identifiziert werden können. Zum einen kann das Elastizitätsdiagramm als Instrument der Zeitreihenanalyse eingesetzt werden. Zum anderen eignet es sich zur Steuerung ökonomischer Größen, zum Beispiel im Rahmen der Preispolitik.
Hintergrund
Elastizitäten können allgemein als Ursache-Wirkungszusammenhang zweier ökonomischer Größen im Sinne einer Reagibilitätsbetrachtung definiert werden. Am häufigsten werden relative Änderungen in ein Verhältnis gesetzt, zum Beispiel bei Preis-Absatz-Funktionen. Es lassen sich allerdings auch Differenzenquotienten bilden, die absolute Größen in eine Beziehung setzen. Erstmals tauchte der Begriff im Rahmen des so genannten Elastizitätskonzepts im Zusammenhang der Analyse von Zinsänderungsrisiken auf.[1] Damit wird eher dem Preisempfinden aus Sicht von Kunden entsprochen, etwa bei Bankprodukten.
Häufig stehen dabei Preisreaktionen von Unternehmen (Banken, Mineralölkonzerne etc.) auf die Veränderung von Marktpreisen (Rohölpreis, Zinsen am Geld- und Kapitalmarkt) im Mittelpunkt. Eine Elastizität von 0,6 bedeutet zum Beispiel, dass ein Unternehmen auf eine Marktpreissteigerung bzw. einen Marktpreisrückgang um einen Prozentpunkt mit einem 0,6-prozentigen Preisanstieg bzw. mit einem 0,6-prozentigen Preisrückgang reagiert. Die lineare Geradengleichung weist damit folgenden funktionalen Zusammenhang auf:
Preis = 0,6 * Marktpreis + Konstante
Anders als beim klassischen Elastizitätsbegriff werden bei der Zinselastizität keine relativen Veränderungen der abhängigen und der erklärenden Variablen ins Verhältnis gesetzt, sondern absolute Zinsänderungen.
Beschreibung
Da Differenzenquotienten und Elastizitäten als Steigung einer Geraden interpretiert werden können, kann man sie direkt aus der linearen Regressionsgeraden-Gleichung ablesen:[2]
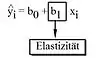
- xi: ökonomische Ursachengröße
- yi: ökonomische Wirkungsgröße
- b0: Achsenabschnitt
- b1: Steigung, Reagibilität oder Elastizität der Kausalbeziehung
Die Analyse kausaler Abhängigkeiten mit Hilfe von Elastizitäten soll an einem Beispiel demonstriert werden. Für diese Inanspruchnahme des Kreditrahmens bei einem Girokonto stellt die Bank Zinsen in Rechnung, deren Höhe von den kurzfristigen Zinssätzen (also Zinssätzen mit einer täglich neu festlegbaren Zinsbindung) an den Geld- und Kapitalmärkten abhängt (vgl. Revolvierender Kredit). Es existiert also ein Kausalzusammenhang zwischen der Zinsentwicklung an den Finanzmärkten und den Zinssätzen, den die Banken bei ihren Kunden ansetzen. In der Abbildung sind die Zinssätze für Überziehungskredite und dem Geldmarktzins EURIBOR seit 2003 dargestellt.
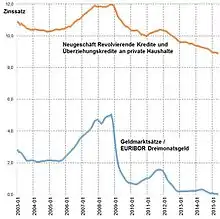
Der Zusammenhang soll mit Hilfe der einfachen linearen Regression analysiert werden. „Einfach“ bedeutet in diesem Zusammenhang, dass die zu erklärende Variable (der Überziehungszins) in Abhängigkeit von nur einer Referenzgröße (Geldmarktzins) in Beziehung gesetzt wird. Mehrfache lineare Regression würde vorliegen, wenn man zur Erklärung des Kontokorrentzinses beispielsweise einen Geldmarktzins und das Konsumklima heranziehen würde.[3]
Die Zeitreihe aus Abbildung 1 wird derart in ein kartesisches Koordinatensystem übertragen, dass auf der x-Achse die unabhängige Variable (Marktzins), auf der y-Achse die abhängige Variable (Positionszins) abgetragen werden. Für jeden Zeitpunkt gibt es eine entsprechende Kombination der beiden Größen, die als Punkt im Diagramm sichtbar gemacht wird.[4] Überträgt man sämtliche Beobachtungswerte der Zeitreihe, entsteht eine Punktwolke, aus der man bereits die Form der Abhängigkeit erkennen kann.
Die obere Grafik (Abbildung 2) zeigt ein solches auch als Streuungsdiagramm bezeichnetes Koordinatensystem. Eine derartige Anordnung der Punkte deutet auf eine positive Regression der Variablen hin, d. h. mit steigenden Geldmarktzinsen als verursachender Variable erhöhen sich auch die Kunden-Zinsen.[5]
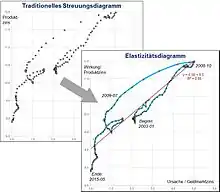
Durch die Punktwolke wird bei der Regressionsanalyse nach dem Verfahren der Kleinsten-Quadrate-Methode eine Gerade gelegt, deren Steigung der gesuchten Elastizität entspricht. Das Elastizitätsdiagramm unterscheidet sich vom „traditionellen“ Streuungs- bzw. Punktdiagramm letztendlich allein dadurch, dass die Kombinationspunkte der jeweils folgenden Zeitpunkte durch Linien miteinander verbunden werden.[6] Die originäre Zeitreihe wird somit in keiner Weise geändert oder verfälscht.
Der große Vorteil ist, dass die Verbindungslinien von Monat zu Monat Anpassungspfade im Diagramm bilden, mit denen Aussagen über das dynamische Verhalten der Variablen ermöglicht werden. Das Ergebnis ist eine differenziertere Elastizitätsbetrachtung, die nicht nur für die Vergangenheit konsistente Werte liefert, sondern auch vielfältige Interpretationen der Ursache-Wirkungsbeziehung zulässt.[7]
Verzögerungseffekte im Elastizitätsdiagramm
Ein rein proportionales Verhalten ist in der betrieblichen Praxis jedoch nur selten anzutreffen, da in ökonomischen Systemen häufig die Wirkung der Ursache in teilweise erheblichem Zeitabstand nacheilt. Es existieren vielmehr eine Vielzahl von Anpassungsmechanismen, die die zeitliche Reaktion des Systems auf eine Änderung der Eingangsgröße beschreiben. Ein solches dynamisches Verhalten wird als Verzögerung oder Time Lag bezeichnet.[8]
Bei der folgenden Betrachtung soll dieser Verzögerungseffekt an idealisierten Preis-Zeitreihen in Form von Sinuswellen demonstriert werden. Sie haben den Vorteil, dass sie ausschließlich systematische Zeitreihenkomponenten enthalten, also frei von stochastischen Einflüssen sind. Daneben lassen sie sich mit nur wenigen Parametern darstellen. Der Marktpreis wird derart als Sinuskurve dargestellt, dass Preissteigerungen sowie -senkungen durchlaufen werden. Die Zeitreihe des Produktpreises wird mit exakt der gleichen Sinusfunktion realisiert (gleiche Amplitude), allerdings wird diese um zwei bzw. vier Tage auf der x-Achse in die Zukunft verschoben, um die Verzögerung bei der Preisanpassung zu simulieren (s. Abb. 3).
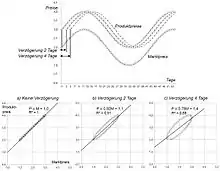
Die Zeitreihen aus Abb. 3 werden nun in ein kartesisches Koordinatensystem übertragen mit der x-Achse als unabhängiger Variable (Marktpreis) und auf der y-Achse als abhängiger Variable (Produktpreis). Für jeden Zeitpunkt gibt es eine entsprechende Kombination der beiden Größen, die als Punkt im Diagramm sichtbar gemacht wird. Die Anpassungspfade in mit zunehmender Verzögerung stärker ausgeprägten Schleifenformen sind typisch für Verzögerungen (s. Abb. 3). Durch die elliptische Anordnung der Preiskombinationen erhöht sich der Abstand und mit ihm das Maß zur Erklärung der Regressionsgeraden. Ein problematischer (Neben-)Effekt ergibt sich dadurch, dass die Steigung der Regressionsgeraden und damit die Elastizität durch systematische Verzerrung den ökonomischen Zusammenhang nicht mehr richtig wiedergibt. So liegt die Elastizität bei einem Time-Lag von nur zwei Tagen nicht mehr bei 1,00, sondern bei 0,91 (0,68 bei vier Tagen), obwohl es sich um identische, allerdings zeitversetzte Reihen handelt.
Einzelnachweise
- Bernd Rolfes (1985): Die Steuerung von Zinsänderungsrisiken in Kreditinstituten. Frankfurt am Main
- Rolfes, B./ Schwanitz, J. (1992): Die „Stabilität“ von Zinselastizitäten, in: Die Bank, Heft 6, S. 334–337
- Johannes Schwanitz: Elastizitätsorientierte Zinsrisikosteuerung in Kreditinstituten, S. 62, Schriftenreihe des Zentrums für Ertragsorientiertes Bankmanagement, Münster; begründet und herausgegeben von H. Schierenbeck und B. Rolfes, Frankfurt am Main 1996
- Schween, Olaf (1998): Zinsänderungsrisiken im Commercial Banking: Eine Value at Risk-basierte Analyse für das Bilanzstrukturmanagement, S. 71, Gabler Verlag
- Schwanitz, Johannes (1995): "Analyse des Kontokorrentzinses mit Hilfe des Elastizitätsdiagramms", S. 166 in: Die Bank 3/95
- Rümmele, Andreas (2009): Zinsanpassungsverhalten von Banken bei der Festlegung von Zinssätzen im Retailbanking, Band 34, S. 64
- Johannes Schwanitz: Elastizitätsorientierte Zinsrisikosteuerung in Kreditinstituten, S. 82, Schriftenreihe des Zentrums für Ertragsorientiertes Bankmanagement, Münster; begründet und herausgegeben von H. Schierenbeck und B. Rolfes, Frankfurt am Main 1996
- Schierenbeck, Henner (2001): Ertragsorientiertes Bankmanagement, S. 138, Band 2: Risiko-Controlling und integrierte Rendite-/Risikosteuerung, 7. Auflage, Gabler Verlag