Durchschlagskraft
Die Durchschlagskraft oder Durchschlagkraft ist die Fähigkeit eines einschlagenden Objekts, im Einschlagsziel einen bestimmten Weg zurückzulegen, bevor es gestoppt wird. Falls das Objekt einen eigenen Antrieb, z. B. Raketenantrieb, hat, ist damit der Weg bis zu dem Punkt gemeint, bei dem sich die Vortriebskraft und die Bremswirkung des Mediums in einem Gleichgewicht befinden. Diese Fähigkeit wird gemeinhin als Durchschlagskraft oder Durchschlagsleistung bezeichnet, auch wenn es sich um keine Kräfte und Leistungen im Sinne der physikalischen Größen handelt.
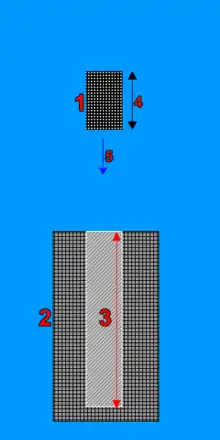
Die Penetration von Panzerungen durch ein Projektil bzw. durch seine Bewegungsenergie ist ein zentrales Forschungsthema der Wehrtechnik.
Durchschlagskraft nach Newton
Die zu erwartende Tiefe des Eindringens in Gase und Flüssigkeiten kann nach Newton unter Vernachlässigung einiger der zahlreichen in der Praxis wirksamen Parameter abgeschätzt werden. Als einzige Parameter werden die Dichte des Mediums sowie die Dichte und die Länge des Impaktors betrachtet. Es wird auch vorausgesetzt, dass der Impaktor seine Form nicht ändert und dass das Medium ein strukturloses Fluid ist. Die Form des Impaktors und andere aero- und hydrodynamische Effekte beim Verdrängen des Mediums bleiben unberücksichtigt.
Unter diesen Bedingungen dringt ein Impaktor so viele Male seiner eigenen Länge in ein Medium ein, wie seine Dichte im Verhältnis größer ist als die des Mediums. Auf dieser Strecke verdrängt er eine Masse, die seiner eigenen entspricht und überträgt seinen Impuls vollständig an das Medium:
- Eindringtiefe
mit
- Länge des Impaktors
- Dichte Impaktor
- Dichte Medium
Unter diesen Voraussetzungen spielt die Auftreffgeschwindigkeit keine Rolle. Der Impuls des Impaktors wird durch Verdrängung einer Masse aufgebraucht, deren Wert nach dem Impulserhaltungssatz in einem festen Verhältnis zur Masse des Impaktors, also einer geschwindigkeitsunabhängigen Größe, steht. Zur Veranschaulichung können Billardkugeln angeführt werden, bei denen eine vollständige Impulsübertragung bei frontalem Stoß ebenfalls unabhängig von der Geschwindigkeit erfolgt. In Festkörpern bleibt der Impaktor nach vollständigem Übertragen des Impulses stehen. In Fluiden bewegt er sich durch äußere Kräfte, wie die Schwerkraft, weiter.
Beim Auftreffen auf einen Festkörper wird bei der Abschätzung davon ausgegangen, dass der Impaktor durch den Druck beim Aufprall die Festigkeitsgrenze des Materials verlustfrei überwindet, so dass auch hier vereinfacht von einer Verdrängung nach den Gesetzen der Fluiddynamik ausgegangen wird.
Durchschlagskraft in der Praxis


Beim Militär ist die Durchschlagskraft bei der Bekämpfung von beschussgeschützten Zielen (Hartziele) von Bedeutung. Die Durchschlagskraft wird oft in RHA (englisch: rolled homogeneous armour = gewalzte homogene Panzerung) angegeben. Geschosse für die Bekämpfung solcher Ziele sind unter Beachtung der Zusammenhänge konstruiert, die die Durchschlagskraft bestimmen. Da die Durchschlagskraft direkt von der Dichte und dem Verhältnis von Länge und Durchmesser abhängt, enthalten zum Beispiel Wuchtgeschosse einen möglichst lang ausgeformten Kern aus einem dichten, harten Material, oder es sind spezielle pfeilförmige, unterkalibrige APFSDS-Geschosse mit Treibspiegel. Als Materialien werden u. a. Wolframcarbid oder abgereichertes Uran (Uranmunition) verwendet, die eine hohe Dichte bei geringer Verformbarkeit aufweisen. Um die Festigkeitsgrenze von Panzerungen zu überwinden, werden sie mit möglichst hoher Mündungsgeschwindigkeit abgefeuert. Zusätzlich zur reinen Impulsbetrachtung nach Newton kann die Durchschlagskraft bei Panzerungen auch mit Hilfe der Panzerformel abgeschätzt werden.
Für den Einsatz in Infanteriewaffen gibt es Munition mit verbesserter Durchschlagswirkung. Die Durchschlagskraft wird dabei vor allem durch den Einsatz von harten Geschossmaterialien erhöht, die beim Auftreffen auf ein gepanzertes Ziel oder auf eine Schutzweste nur gering deformiert werden. Die Geschosse können massive Messinggeschosse sein oder, wie etwa bei den Geschossen der Patrone 5,45 × 39, einen gehärteten Stahlkern enthalten.
Die Durchschlagswirkung in weichen Zielmedien (Weichziele) hängt von zahlreichen zielballistischen Faktoren ab. Vollmantel- und Massivgeschosse können sich durch die Präzession des Geschosses, die direkt nach dem Abschuss am höchsten ist und dann abnimmt, nach dem Eindringen ins Zielmedium überschlagen und unter Umständen zerbrechen, was die Eindringtiefe kaum vorhersehbar beeinflusst. Durch die Abnahme der Präzession bei steigender Schussentfernung und die dadurch verringerte Neigung zum Überschlagen kann die Durchschlagswirkung bei abnehmender Auftreffgeschwindigkeit zunächst zunehmen. Die Bewegung von Deformationsgeschossen kann durch das Aufpilzen nach dem Eindringen ins Ziel auch bei hoher Geschwindigkeit stabil bleiben.[1] Durch den großen Querschnitt des deformierten Geschosses wird die Bewegungsenergie schnell an das Zielmedium abgegeben, wodurch sich die Durchschlagswirkung verringert. Eine hohe Energieabgabe im Ziel wird in der Regel beim jagdlichen Einsatz angestrebt.
Auch die Durchschlagswirkung panzerbrechender Waffen mit Hohlladung hängt von der Dichte und der Form des penetrierenden Metallstrahls ab. Bei der Explosion der Ladung entsteht aus der Metalleinlage durch Kaltverformung ein Metallstrahl, der eine möglichst große Länge und Dichte aufweisen sollte. Wegen der hohen Geschwindigkeit des Strahls von bis über 10 km/s ist die Härte des Materials nebensächlich, da bei dieser Auftreffgeschwindigkeit die Fließgrenze jedes Materials überschritten wird. Ausschlaggebend ist somit die Dichte, weshalb u. a. Kupfer und Tantal als Metalleinlage zum Einsatz kommen.
Die Regel nach Newton bestimmt auch, welche Größe Meteoriten haben müssen, um nicht auf Geschwindigkeiten von 150–300 km/h (je nach Form) abgebremst zu werden, bevor sie die Erdoberfläche erreichen. Die Dichte von Luft, gemittelt auf die Höhe, in der die Bremswirkung der Atmosphäre einsetzt (ca. 70 km), beträgt etwa 1,75·10−4 g/cm³ . Ein Steinmeteorit mit einem Verhältnis Länge zu Durchmesser von 1:1 und einer typischen Dichte von 3,4 g/cm³ muss demnach eine Größe von mindestens etwa 3,6 Meter haben, um die Erdoberfläche mit einer Geschwindigkeit größer als die o. g. Geschwindigkeit zu erreichen, da das Dichteverhältnis etwas unter 1:20.000 liegt. Eisenmeteoriten mit einer typischen Dichte von 7,8 g/cm³ werden ab einer Größe von etwa 1,5 m nicht mehr auf die Freifallgeschwindigkeit abgebremst.
Spezielle Geschosse wie Bunker Buster können eingesetzt werden, um stark verbunkerte Anlagen zu zerstören. Nach der hier beschriebenen Näherungsformel lässt sich für einen massiven Urankörper (Dichte um 19 g/cm³) von 1 m Länge eine Eindringtiefe von mehr als 6 m in Stein (Dichte etwas mehr als 3 g/cm³) vorhersagen.
Literatur
Die Näherungslösung von Newton für die Durchschlagskraft von Geschossen wird in vielen Standard-Lehrbüchern der Physik behandelt, zum Beispiel in Gerthsen Physik.[2]
Einzelnachweise
- Eisnecker, Finze, Hocke, Skrobanek: Kammer-Diener, 120 Jahre 8x57, Visier, internationales Waffenmagazin Ausgabe 12/2008, S. 6–18.
- Dieter Meschede (Hrsg.): Gerthsen Physik, 22. Auflage, Springer Verlag, ISBN 3-540-02622-3), oder 25. Auflage (2015), Seite 34.