Drehquadrik
Eine Drehquadrik ist in der Mathematik eine Fläche im dreidimensionalen euklidischen Raum, welche sich durch spezielle Symmetrieeigenschaften auszeichnet. Sie lässt sich als Drehfläche zweiter Ordnung charakterisieren.
Drehquadriken gehören zu den Quadriken. Es sind die Überstreichungsflächen von rotierenden Kegelschnitten im dreidimensionalen Raum, also diejenigen Flächen, die überstrichen werden, wenn im dreidimensionalen Raum ein Kegelschnitt um eine seiner Symmetrieachsen rotiert. Wie alle Quadriken lassen sie sich in kartesischen Koordinaten als Mengen von Nullstellen einer quadratischen Gleichung verstehen.
Klassifikation
Es werden folgende Typen von Drehquadriken unterschieden:


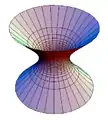 Einschaliges Rotationshyperboloid
Einschaliges Rotationshyperboloid Zweischaliges Rotationshyperboloid
Zweischaliges Rotationshyperboloid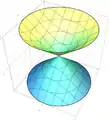

Die beiden letzten Typen weisen Singularitäten auf.
Literatur
- Rudolf Bereis: Darstellende Geometrie. Band I.. Akademie-Verlag, Berlin 1964, XI Drehflächen zweiter Ordnung.
- Rudolf Bereis: Über die Böschungslinien auf Drehquadriken. In: Monatshefte für Mathematik. Band 56, Nr. 4, 1952, S. 344–351, doi:10.1007/BF01302720.
- VRML-Dateien von Drehquadriken. Forum für Geometrie, abgerufen am 4. April 2013.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.