Cremonaplan
Der Cremonaplan dient bei statisch bestimmten Fachwerken der zeichnerischen Bestimmung der Stabkräfte zur Bemessung der Stäbe. Er wurde im 19. Jahrhundert von Antonio Luigi Gaudenzio Giuseppe Cremona entwickelt und 1872 veröffentlicht.[1]
Die dem Cremonaplan zugrundeliegenden Methoden sind sehr hilfreich bei der Techniker- oder Ingenieurausbildung und zum Verständnis der Kräfteverläufe. Im Computerzeitalter erfolgt die Ermittlung der Stabkräfte in der Regel schneller und bequemer ohne die grafische Darstellung des Kraftecks.
Beschreibung
Das Grundprinzip beruht darauf, dass an jedem Knotenpunkt eines Fachwerks Gleichgewicht herrschen muss. Wenn man die Stabkräfte an den Knoten als äußere Kräfte auffasst, ist die Summe dieser Kräfte gleich null. Für jeden Knoten lässt sich ein geschlossenes Krafteck zeichnen (siehe Culmann-Verfahren). Fügt man die einzelnen Kraftecke zusammen, entsteht der Cremonaplan.
Jede Stabkraft kommt an zwei Knoten und in zwei Kraftecken vor. Deshalb ergibt der Cremonaplan ein geschlossenes maßstabsgerechtes Krafteck, in dem jede Stabkraft nur einmal vorkommt.
Notwendige Hilfsmittel
Manuell

Man benötigt ein Blatt Papier, Lineal, Geodreieck, Bleistift, Buntstifte, Anspitzer und Radiergummi. Die Skala auf dem Lineal dient zum Ablesen der Eingangs- und Ausgangsgrößen. Alle Kräfte werden zur grafischen Darstellung mit einem geeigneten Maßstab in Längen umgerechnet. Die größte der zu erwartenden Kräfte bestimmt über den gewählten Maßstab (z. B. „1 cm entspricht 1 kN“) letztendlich die Dimension des Papiers. Im Allgemeinen gilt: je größer die Zeichnung, desto präziser ist die relative Genauigkeit und somit i. d. R. auch das Ergebnis. Vorteil: Stabkräfte können „vor Ort“, ohne Strom und aufwendige Ausrüstung schnell und zuverlässig ermittelt werden. Ein Nachteil ist unter Umständen ein höherer Zeitaufwand.
Rechnergestützt
Eine einfache 2D-CAD-Software (mit nur wenigen Grundfunktionen wie: Linie, Ebene, Parallele, Bemaßung, Messen) genügt für die Erstellung eines Cremonaplanes. Sollten Befehlsmakros für das Erstellen des Kräfteplanes vorhanden sein, so beschleunigt dies die Arbeit erheblich. Durch die hohe Genauigkeit (oftmals 8 bis 16 Nachkommastellen) eines 2D-CAD-Systems sind erstaunlich genaue Berechnungen möglich. Eine solche Genauigkeit ist aber in der praktischen Baustatik nur in Sonderfällen notwendig.
Vorgehensweise
Bei einem statisch bestimmten (idealen) Fachwerk kann man (auch in diesem Fall) auch die Auflagerkräfte mit dem Cremonaplan bestimmen; oftmals werden die Auflagerkräfte schon vorab berechnet, um die Konstruktion nochmals kontrollieren zu können, und weil auch die Konstruktion des Cremonaplanes einfacher wird. Die Bestimmung der Auflagerkräfte bei einem statisch bestimmten System kann im Allgemeinen mit der Statik starrer Körper gelöst werden und ist im Lehrplan von Oberstufenschulen enthalten. Die Bestimmung kann im Allgemeinen z. B. zeichnerisch mit dem Seileckverfahren oder rechnerisch nach den Gleichgewichtsbedingungen , , (siehe auch statisch bestimmt) erfolgen.
Vor Bestimmung der Stabkräfte ist es sinnvoll, vorher eventuelle Nullstäbe nach den dafür geltenden Regeln zu ermitteln. In dem unten stehenden Beispiel sind keine Nullstäbe vorhanden.
Nachfolgend die Auflagerkräfte für das unten stehende Beispiel:
, , .
Für die von außen einwirkenden Kräfte muss ein Umfahrungssinn festgelegt werden (in mathematisch positiver Richtung oder im Uhrzeigersinn). Die danach in der richtigen Reihenfolge eingetragenen Kräfte ergeben dann ein geschlossenes Krafteck.
Sofern vorhanden, ist es im Allgemeinen effizient, einen Knoten zu suchen, an dem maximal zwei unbekannte Kräfte wirken. Die Reihenfolge der Knoten kann beliebig gewählt werden, es ist jedoch vorteilhaft, die Knoten der Reihe nach durchzugehen. Bei jedem weiteren Knoten dürfen, zusätzlich zu den bereits bekannten Stäben, wiederum maximal zwei Stäbe anschließen, deren Stabkraft noch nicht bestimmt ist. Bei jeder Kraft kennzeichnet man, zu welchem Stab sie gehört und ob es eine Zug- oder eine Druckkraft ist.
An allen Fachwerkknoten muss man den gleichen Umfahrungssinn verwenden. Es ergibt sich automatisch, dass jede Stabkraft nur einmal gezeichnet zu werden braucht. Da das Krafteck maßstäblich ist, kann man die Längen abmessen und in die entsprechenden Kräfte umrechnen.
In allen Kraftecken sind die Richtungen der Kräfte relevant.
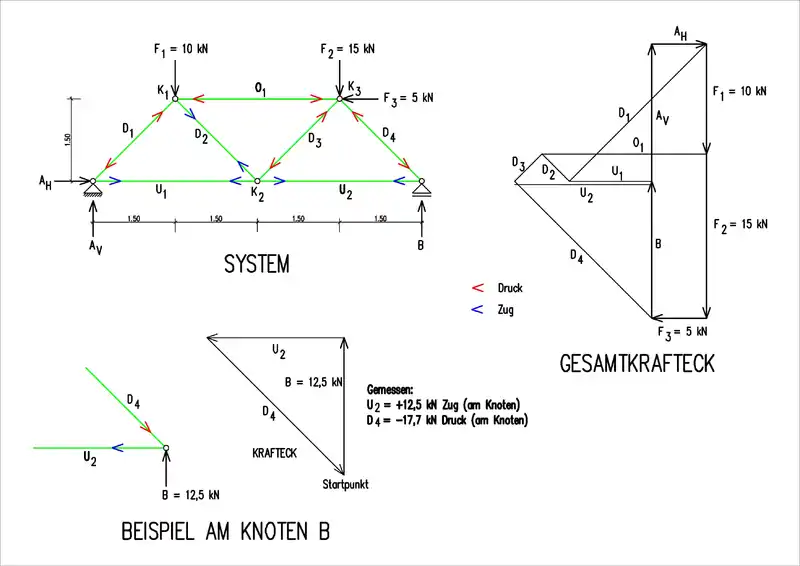
Nachfolgend wird an dem o. a. Beispiel die Ermittlung der Größe und Richtung der Stabkräfte erklärt:
Sofern man die Auflagerkräfte rechnerisch und nicht mit dem Cremonaplan bestimmt, zeichnet man die Auflagerkräfte in das Krafteck der äußeren Kräfte. Es ist vorteilhaft, aber nicht notwendig, sich einen Knoten, bei dem maximal zwei Stabkräfte unbekannt sind, zu suchen. Im Beispiel wurde der Knoten B mit den beiden unbekannten Stabkräften für U2 und D4 gewählt. Zur besseren Übersicht wurde das Einzelkrafteck hier einmal herausgezeichnet.
- Man stellt sich gedanklich zwischen die beiden unbekannten Stäbe und dreht sich (hier rechtsherum) um den Knoten. Die erste (und an diesem Knoten auch einzige) bekannte Kraft ist hier die Auflagerkraft B, die man – hier im Einzelkrafteck – mit ihrer Richtung und Größe maßstäblich aufzeichnet.
- Als Nächstes trifft man den unbekannten Stab U2. An das Ende der vorgehenden Kraft (B) trägt man im Krafteck nun die Wirkungslinie (Richtung der Kraft) als Gerade, noch ohne Größe, an.
- Die jetzt noch verbleibende Kraft im Stab D4 wird im Krafteck ebenfalls mit ihrer Wirkungslinie angetragen. Da sie das Krafteck schließen muss, geht sie hier durch den Anfangspunkt der Auflagerkraft B.
- Jetzt hat man das fertige Krafteck B, U2, D4. Da sich das Krafteck schließen muss, kann man die Richtungspfeile entsprechend antragen. Die Größe der Stabkräfte lässt sich durch Messen der einzelnen Längen im gewählten Maßstab ermitteln.
- In der Systemskizze am untersuchten Knoten trägt man jetzt ebenfalls die ermittelten Pfeile in derselben Richtung an. Hier in Knoten B geht die Kraft U2 vom Knoten weg und die Kraft D4 zum Knoten hin. Kräfte vom Knoten weg sind im Stab immer Zugkräfte (hier blau) und zum Knoten hin immer Druckkräfte (hier rot). Nun hat man für den untersuchten Knoten die Größe und Richtung der Kräfte ermittelt.
- Da die Kräfte im jeweiligen Stab bezüglich Richtung und Größe konstant sind, kann man jetzt die Richtungspfeile am gegenüberliegenden Knoten der beiden Stäbe antragen: Zugkräfte vom Knoten weg, Druckkräfte zum Knoten hin. Die Pfeile zeigen an den Stabenden also in die entgegengesetzte Richtung. Damit ist der Knoten B fertig.
- Jetzt kann man die Kräfte am nächsten Knoten ermitteln. Im Beispiel wäre das der Knoten K3 mit den bekannten Lasten F2, F3 und Stabkraft D4 und den unbekannten zwei Stäben D3 und O1. Man geht dafür sinngemäß vor wie unter Punkt 1 bis Punkt 6 beschrieben.
Man muss nicht für jeden Knoten ein eigenes Krafteck zeichnen, sondern kann, mit etwas Übung, alle Stabkräfte in dem Gesamtkrafteck ermitteln. Hier hat man am Ende auch eine Kontrolle, da sich das Gesamtkrafteck schließen muss.
Siehe auch
Literatur
- Luigi Cremona: Le figure reciproche nella statica grafica. Ulrico Hoepli, Mailand 1872.
- Gross, Hauger, Schröder, Wall: Technische Mechanik 1. Springer Verlag.
Einzelnachweise
- Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin, ISBN 978-3-433-03229-9, S. 456.