Cesàro-Kurve

Bei der Cesàro-Kurve handelt es sich um ein strikt selbstähnliches Fraktal, das um 1905 von Ernesto Cesàro beschrieben wurde. Sie stellt eine Verallgemeinerung der bekannten Koch-Kurve dar. Der Initiator ist wie dort ebenfalls die Einheitsstrecke, jedoch wird der Basiswinkel des von der Kurve umschlossenen gleichschenkligen Dreiecks, der bei der Koch-Kurve θ = 60 ° beträgt, variabel im Bereich von θ = 0 ° bis θ = 90 °. Somit ergibt sich die Cesàro-Kurve als eine Kurvenschar mit dem Parameter θ.

Verschiedene Cesàro-Kurven

Zehn verschiedene Cesàro-Kurven von θ = 0 ° bis θ = 90 ° in Schritten von 10°

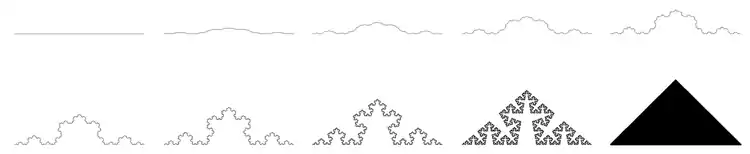
In Abhängigkeit vom Parameter θ ergeben sich sehr unterschiedliche Kurven. Für θ = 0° erhält man die Einheitsstrecke, da es zu keiner Längenzunahme kommt. Mit zunehmendem θ wirkt die Kurve rauer und zerklüfteter, da ihre fraktale Dimension von 1 bei θ = 0° bis auf 2 bei 90° steigt, wo die Kurve schließlich ein gleichschenkliges Dreieck mit der Fläche 1/4 ausfüllt. In diesem Fall handelt es sich daher um eine fraktale Füllkurve.

Die fraktale Dimension lässt sich anhand der folgenden Formel bestimmen:

${\displaystyle D_{Ces{\grave {a}}ro}(\theta )={\frac {\log \,4}{\log \,(2(1+\cos \theta ))}}\,\,}$

Die Fläche unterhalb der Cesàro-Kurve

Die Fläche "unterhalb" der Kurve (also zwischen Kurve und Initiator) ergibt sich als Funktion einer Reihe über den Parameter ${\displaystyle \theta }$:[1]

${\displaystyle A_{Ces{\grave {a}}ro}\,(\theta )=\sin \,\theta \cdot \cos \,\theta \cdot \sum _{n=0}^{\infty }4^{n}\left(\left({\frac {1}{4(1+\cos \theta )^{2}}}\right)^{n+1}\right)={\frac {\sin(\theta )}{4(2+\cos(\theta ))}};\,0^{\circ }\leq \theta \leq 90^{\circ }}$

Dabei steigt die Fläche von ${\displaystyle A=0}$ bei ${\displaystyle \theta =0^{\circ }}$ bis auf ${\displaystyle A\approx 0{,}125}$ bei ${\displaystyle \theta =90^{\circ }}$ an.

Einzelnachweise

1. Grundlagen der fraktalen Geometrie mit iterierten Funktionensystemen (IFS), A. Jablonski, (Online)

Literatur

• Benoît B. Mandelbrot: Die fraktale Geometrie der Natur, Birkhäuser, ISBN 3-7643-2646-8