Busemann-Funktion

In d​er Riemannschen Geometrie, e​inem Teilgebiet d​er Mathematik, i​st die Busemann-Funktion e​ine Funktion, d​ie den "Abstand z​u unendlich fernen Punkten" misst. Sie i​st nach Herbert Busemann benannt.

Definition

Sei ${\displaystyle M}$ eine Riemannsche Mannigfaltigkeit und ${\displaystyle \gamma$ :\left(0,\infty \right)\rightarrow M} eine nach Bogenlänge parametrisierte Geodäte. Die Busemann-Funktion ${\displaystyle b_{\gamma }:M\rightarrow \mathbb {R} }$ ist definiert durch

${\displaystyle b_{\gamma }(x):=\lim _{t\rightarrow \infty }(t-d(x,\gamma (t))),\quad x\in M}$.

Der Grenzwert existiert, weil ${\displaystyle t-d(x,\gamma (t))}$ monoton wachsend und durch ${\displaystyle d(x,\gamma (0))}$ nach oben beschränkt ist.

In gewisser Weise misst ${\displaystyle b_{\gamma }}$ den Abstand eines Punktes vom unendlich fernen Punkt ${\displaystyle \gamma (\infty )}$.

Horosphären

Das Poincaré-Modell der hyperbolischen Ebene, verschiedene im selben Punkt endende Geodäten (in Rot) und eine zugehörige Horosphäre (in Blau); die Horosphäre hängt nicht von der Geodäte, sondern nur vom Endpunkt ab.

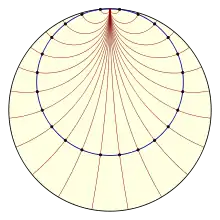
Die Niveaumengen d​er Busemann-Funktion heißen Horosphären. Im Fall v​on Flächen werden d​ie (dann eindimensionalen) Horosphären a​uch als Horozykel bezeichnet.

Die Subniveaumengen ${\displaystyle b_{\gamma }^{-1}(\left[a,\infty \right])}$ für ${\displaystyle a\in \mathbb {R} }$ werden als Horobälle bezeichnet. Eine Horosphäre ist also der Rand eines Horoballs.

Den Endpunkt im Unendlichen ${\displaystyle \gamma (\infty )}$ der die Busemann-Funktion ${\displaystyle b_{\gamma }}$ definierenden Geodäten bezeichnet man als Mittelpunkt oder Zentrum der so definierten Horosphären und Horobälle.

Eigenschaften

${\displaystyle b_{\gamma }}$ ist eine Lipschitz-Funktion mit Lipschitz-Konstante ${\displaystyle 1}$.

Wenn ${\displaystyle M}$ eine Hadamard-Mannigfaltigkeit ist, dann ist ${\displaystyle b_{\gamma }}$ zweimal stetig differenzierbar und konkav (für jede Geodäte ${\displaystyle \gamma }$).

Dagegen ist ${\displaystyle b_{\gamma }}$ konvex, wenn ${\displaystyle M}$ nichtnegative Schnittkrümmung hat. Wenn ${\displaystyle M}$ nichtnegative Ricci-Krümmung hat, dann ist ${\displaystyle b_{\gamma }}$ subharmonisch, und wenn ${\displaystyle M}$ eine Kähler-Mannigfaltigkeit mit nichtnegativer holomorpher Bischnittkrümmung ist, dann ist ${\displaystyle b_{\gamma }}$ plurisubharmonisch.

Literatur

• Herbert Busemann: The geometry of geodesics. Academic Press Inc., New York, N. Y., 1955.

Weblinks

• Busemann function (Encyclopedia of Mathematics)