Bremsvermögen
Das Bremsvermögen (englisch: Stopping Power) eines Materials ist die kinetische Energie, die ein geladenes Teilchen pro Weglängeneinheit beim Eindringen in das Material verliert, gemessen beispielsweise in MeV/cm (siehe Bild). Die Energie wird in verschiedenartigen Stoßprozessen aufgezehrt. Das Bremsvermögen hängt ab von der Teilchenart, der augenblicklichen Teilchenenergie sowie Art und Dichte des Materials.
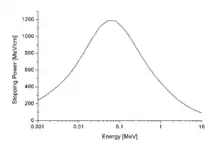
Bremsvermögen, Bragg-Peak und Reichweite
Alle elektrisch geladenen Teilchen verlieren Energie beim Durchgang durch Materie. Im Folgenden werden vor allem positive Ionen betrachtet. Der Ausdruck Bremsvermögen beschreibt die Situation sozusagen vom Standpunkt des bremsenden Materials aus, während Energieverlust pro Weglängeneinheit sich auf das Teilchen bezieht. In Bezug auf Einheit und Zahlenwert sind beide Größen identisch. Der Energieverlust pro Weglängeneinheit wird üblicherweise mit negativem Vorzeichen geschrieben:
wobei E die Energie und x die Weglänge bedeuten. Infolge des Minuszeichens ist S eine positive Größe. Meistens steigt der Energieverlust pro Wegeinheit während des Weges, den das Teilchen zurücklegt, an. Die Kurve, die dies beschreibt, heißt Bragg-Kurve (benannt nach William Henry Bragg). Kurz vor dem Ende des Weges durchläuft der Energieverlust pro Wegeinheit ein Maximum, den Bragg-Peak, und fällt dann abrupt auf (fast) Null ab. Dies ist von großer praktischer Bedeutung bei der Strahlentherapie.
Die obige Gleichung beschreibt das lineare Bremsvermögen, das zum Beispiel in MeV/mm gemessen wird. Dividiert man das lineare Bremsvermögen durch die Dichte des Materials, so erhält man das Massenbremsvermögen, das beispielsweise in MeV/(mg/cm2) gemessen wird. Das Massenbremsvermögen ist unabhängig von der Materialdichte.
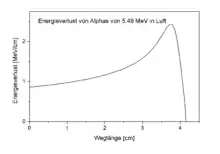
Das Bild zeigt, wie das Bremsvermögen von Luft – und damit auch die Ionisationsdichte – für Alphateilchen entlang des Weges zunimmt, bis sie das Maximum erreicht. 5,49 MeV ist die Energie der Alphateilchen aus dem natürlichen Radongas (Radon-222), das überall vorkommt, wo es Granit im Boden gibt.
Der Weg, den die Teilchen zurücklegen, bis ihre Energie auf Null sinkt, heißt Reichweite. Die Reichweite ist abhängig von der Teilchenart, von der Anfangsenergie und vom Material. Man kann die Reichweite näherungsweise unter Vernachlässigung der Zufälligkeit der Energieabgabe berechnen, indem man das reziproke Bremsvermögen über die Energie (von der Anfangsenergie bis Null) integriert (engl. continuous slowing down approximation, CSDA):
Die so berechnete CSDA-Reichweite ist zu unterscheiden von der Eindringtiefe in ein Medium. Diese ist für leichte Teilchen wie Elektronen merklich kürzer als die „ausgestreckte“ CSDA-Reichweite, weil die Teilchen auf ihrem Weg durch Streuung an den Atomen abgelenkt werden, so dass sich eine Zickzack-Bewegung ergibt.
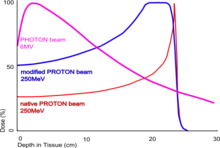
Das dritte Bild zeigt die Energiedeposition eines Protonenstrahls von 250 MeV in Wasser (orangefarbene Kurve); die Kurve hat einen sehr spitzen Bragg-Peak. Die blaue Kurve zeigt die gesamte Energiedeposition bei mehreren aufeinanderfolgenden Protonenbestrahlungen mit variierenden Energien. Solche Protonenstrahlen werden bei der Strahlentherapie ausgedehnter Tumoren genutzt, da hierbei der größte Teil der Energiedeposition und damit auch der Schädigung im Tumor selbst stattfindet.
Das Bild zeigt zum Vergleich auch die Absorption eines hochenergetischen Photonenstrahls. Diese Kurve ist gänzlich anders (im Wesentlichen eine exponentielle Abnahme), da das Photon nicht durch viele Stöße allmählich Energie abgibt, sondern meist in einem einzigen Ionisationsprozess seine ganze Energie verliert (siehe auch Strahlung). Die Absorption eines Photonenstrahls wird nicht durch das Bremsvermögen beschrieben, sondern durch einen Absorptionskoeffizienten.
Die englischen Ausdrücke Stopping Power und Bragg-Peak sind auch im Deutschen sehr üblich.
Elektronisches und nukleares Bremsvermögen
Unter elektronischem Bremsvermögen versteht man die Abbremsung durch unelastische Stöße zwischen dem schnellen Ion und den Elektronen des durchquerten Mediums. Diese Stöße können Anregung und Ionisation sowohl der Elektronen des Mediums als auch der Elektronen des Ions bewirken.
Mit einer Genauigkeit von einigen Prozent kann man das elektronische Bremsvermögen oberhalb einer spezifischen Energie von einigen hundert keV pro Nukleon theoretisch berechnen, beispielsweise durch die Bethe-Formel. Für niedrigere Energien wird die Berechnung schwieriger.[1]
Graphische Darstellungen von gemessenen Werten des elektronischen Bremsvermögens für viele Ionen in vielen verschiedenen Substanzen sind dokumentiert.[2] Die Genauigkeit verschiedener Tabellen zum Bremsvermögen wurde mit Hilfe statistischer Methoden unter anderem von Helmut Paul untersucht.[3]
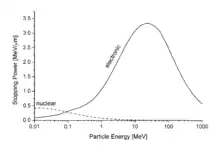
Unter nuklearem Bremsvermögen versteht man elastische Stöße zwischen dem Ion und den Atomen des Materials (der Ausdruck "nuklear" hat hier nichts mit nuklearen Kräften, also Kernkräften zu tun). Wenn man die Form des abstoßenden Potentials zwischen Ion und Atom kennt, kann man das nukleare Bremsvermögen berechnen. In dem oben gezeigten Bild für Protonen in Aluminium ist der nukleare Beitrag überall vernachlässigbar, außer bei der kleinsten Energie. Mit steigender Masse des Ions wächst aber der nukleare Beitrag. In der hier rechts gezeigten Figur ist bei kleiner Energie der nukleare Beitrag größer als der elektronische.
Bei nicht zu hohen Energien ist das Bremsvermögen daher die Summe zweier Größen: . Es gibt verschiedene semi-empirische Modelle zur Berechnung des Bremsvermögens. Das Modell von Ziegler, Biersack und Littmark wurde ursprünglich in einem Buch[4] beschrieben. Die neueste Version des Programms[5][6] wird heute sehr viel verwendet.
Jenseits des Maximums nimmt das Bremsvermögen ungefähr proportional mit steigender Geschwindigkeit ab, nach dem Durchlaufens eines Minimums bei relativistischen Geschwindigkeiten aber wieder zu[7]. Teilchen mit dieser Geschwindigkeit heißen minimal ionisierende Teilchen (englisch: minimum ionizing particle, mip).
Gitterführungseffekt (Channeling)
Abweichungen vom üblichen Bremsvermögen treten in monokristallinen Festkörpern auf. Bei nicht zu kleinen Energien führt die regelmäßige Anordnung der Gitteratome hier zu einer Veränderung der Stoßwahrscheinlichkeiten, die dann stark von der Einfallsrichtung der Teilchen relativ zur Ausrichtung des Kristalls abhängen.
Literaturzitate
- P. Sigmund, Particle Penetration and Radiation Effects. Springer Berlin Heidelberg New York, 2005
- Helmut Paul: Stopping Power for Light and Heavier Ions - Graphs, Data, Comments and Programs, abgerufen am 18. April 2015.
- Helmut Paul: A comparison of recent stopping power tables for light and medium-heavy ions with experimental data, and applications to radiotherapy dosimetry. In: Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 247, 2006, S. 166–172, doi:10.1016/j.nimb.2006.01.059.
- J. F. Ziegler, J. P. Biersack, and U. Littmark, The Stopping and Range of Ions in Matter, volume 1, Pergamon, New York, 1985.
- J. F. Ziegler: SRIM & TRIM
- J. F. Ziegler, J. P. Biersack, and M. D. Ziegler: SRIM - The Stopping and Range of Ions in Matter. SRIM Co., 2008. ISBN 0-9654207-1-X
- http://pdg.lbl.gov/2005/reviews/passagerpp.pdf
Weblinks
- Durchgang geladener Teilchen durch Materie, inklusive Plot (engl.; PDF-Datei; 512 kB)
- Stopping Power: Daten und Kurven (Memento vom 6. Februar 2012 im Internet Archive) (engl.) Diese Version ist nicht aktuell. Für die aktuelle Version s. o. unter Literaturzitaten.