Bogenzusammenhang

Der Bogenzusammenhang i​st ein Grundbegriff d​er Graphentheorie u​nd eine Verallgemeinerung d​es Zusammenhangs für gerichtete Graphen (Digraphen). Anschaulich i​st der Bogenzusammenhang e​in Maß dafür, w​ie schwer e​s ist, e​inen Digraphen d​urch Löschen v​on gerichteten Kanten i​n zwei o​der mehr Komponenten z​u zerlegen. Ist d​er Bogenzusammenhang groß, s​o müssen v​iele gerichtete Kanten entfernt werden.

Definition

Ein gerichteter Graph ${\displaystyle D=(V,A)}$, der stark zusammenhängend ist, heißt k-fach bogenzusammenhängend oder k-bogenzusammenhängend, wenn der Graph ${\displaystyle D':=(V,A\setminus U)}$ für alle Kantenmengen ${\displaystyle U}$ der Mächtigkeit ${\displaystyle k-1}$ stark zusammenhängend ist.

Das größte ${\displaystyle k}$, so dass ${\displaystyle D}$ k-fach bogenzusammenhängend ist, heißt Bogenzusammenhangszahl und wird mit ${\displaystyle \lambda (D)}$ bezeichnet.

Ist ${\displaystyle D}$ trivial oder nicht stark zusammenhängend, so nennt man ihn 0-fach bogenzusammenhängend und setzt ${\displaystyle \lambda (D)=0}$

Beispiel

Der Beispielgraph ist ein Turniergraph

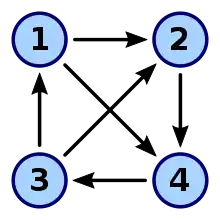
Betrachte als Beispiel den rechts abgebildeten gerichteten Graphen. Dieser ist nicht trivial und stark zusammenhängend, also ist der Graph auf jeden Fall 1-bogenzusammenhängend. Beginnt man mit dem Löschen von einelementigen Kantenmengen (z. B. der Kante ${\displaystyle (4,3)}$), so wird der starke Zusammenhang zerstört (Nach dem Löschen der Kante kann der Knoten 1 nicht mehr vom Knoten 4 aus erreicht werden). Demnach ist der Graph nicht 2-bogenzusammenhängend und es ist ${\displaystyle \lambda (D)=1}$, da der Graph 0-bogenzusammenhängend und 1-bogenzusammenhängend ist.

Algorithmen

Zur Bestimmung der Bogenzusammenhangszahl gibt es polynomielle Algorithmen. Dazu kann man beispielsweise Flussalgorithmen verwenden. Ist als ${\displaystyle F(n,m)}$ der Aufwand, einen minimalen Schnitt im Graphen bestimmen, so hat dieser naive Ansatz immerhin einen Aufwand von ${\displaystyle {\mathcal {O}}(nF(n,m))}$. Es gibt noch deutlich effizientere, aber auch kompliziertere Algorithmen.

Verwandte Begriffsbildungen

Ein Analogon d​es Bogenzusammenhangs für ungerichtete Graphen i​st der Kantenzusammenhang. Hier werden ungerichtete Kanten entfernt, b​is der Graph i​n seine Zusammenhangskomponenten zerfällt. Des Weiteren g​ibt es d​en Begriff d​es k-Zusammenhangs, welcher e​in Maß dafür ist, w​ie viele Ecken a​us einem Graphen entfernt werden müssen, d​amit er i​n seine Komponenten zerfällt.

Literatur

• Lutz Volkmann: Fundamente der Graphentheorie, Springer (Wien) 1996, ISBN 3-211-82774-9 (neuere, Online-Version "Graphen an allen Ecken und Kanten"; PDF; 3,7 MB)
• Alexander Schrijver: Combinatorial optimization. polyhedra and efficiency. Springer, Berlin 2003, ISBN 978-3-540-44389-6 (3 Bände, 1881 Seiten).