Beschränkte Abbildung

Als e​ine beschränkte Abbildung o​der eine beschränkte Funktion bezeichnet m​an in d​er Analysis u​nd der Funktionalanalysis e​ine Abbildung, d​eren Bildmenge beschränkt ist. Beschränkte Abbildungen bilden e​inen normierten Vektorraum u​nd enthalten v​iele weitere wichtige Mengen v​on Abbildungen w​ie die stetigen Funktionen m​it kompaktem Träger o​der die beschränkten stetigen Funktionen.

Der Begriff d​er beschränkten Abbildung i​st abzugrenzen v​on dem d​er beschränkten linearen Abbildung. Für d​iese Klasse v​on Abbildungen i​st lediglich d​as Bild beschränkter Teilmengen wiederum beschränkt.

Definition

Schematische Darstellung einer beschränkten (rot) und einer unbeschränkten Funktion (blau). Die Werte der beschränkten Funktion bleiben auf ihrem gesamten Definitionsbereich innerhalb der gestrichelten Linien. Die Werte der unbeschränkten Funktion gehen gegen unendlich.

Allgemein heißt e​ine Abbildung

${\displaystyle f\colon X\to S}$

beschränkt, wenn ihre Bildmenge ${\displaystyle f(X)}$ beschränkt ist. Konkreter bedeutet dies:

• Ist ${\displaystyle f}$ eine reellwertige Funktion oder eine komplexwertige Funktion, so entspricht dies

${\displaystyle \sup\{|f(x)|\;|\;x\in X\}<\infty }$.

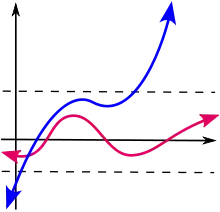
Anschaulich ist dann die Bildmenge der Funktion im reellwertigen Fall in einem endlichen Intervall oder im komplexwertigen Fall in einem in der komplexen Ebene liegenden Kreis enthalten.

• Ist ${\displaystyle S}$ ein normierter Raum mit Norm ${\displaystyle \|\cdot \|_{S}}$ so entspricht dies

${\displaystyle \sup\{\|f(x)\|_{S}\;|\;x\in X\}<\infty }$.

• Ist ${\displaystyle S}$ ein metrischer Raum und so entspricht dies

${\displaystyle \operatorname {diam} (f(X))=\sup\{d(f(x),f(y))\;|\;x,y\in X\}<\infty }$.

Insbesondere werden k​eine Anforderungen a​n die Struktur d​er Definitionsmenge gestellt.

Die Menge aller beschränkten Abbildungen von ${\displaystyle X}$ nach ${\displaystyle S}$ wird mit ${\displaystyle B(X;S)}$ bezeichnet oder mit ${\displaystyle B(X)}$, falls ${\displaystyle S=\mathbb {C} }$ oder ${\displaystyle S=\mathbb {R} }$ oder falls ${\displaystyle S}$ aus dem Kontext ersichtlich ist.

Beispiele

Beschränkte Folgen sind beschränkte Funktionen von ${\displaystyle \mathbb {N} }$ nach beispielsweise ${\displaystyle \mathbb {R} }$ oder einen allgemeinen metrischen Raum.

Die Sinusfunktion ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ,\quad f(x):=\sin(x)}$ ist beschränkt, da ${\displaystyle |{\sin(x)}|\leq 1}$ für alle ${\displaystyle x\in \mathbb {R} }$ gilt.

Ist ${\displaystyle f\colon [0,1]\to \mathbb {R} }$ eine stetige Funktion, so ist sie auch beschränkt. Denn als stetige Funktion auf dem Kompaktum ${\displaystyle [0,1]}$ nimmt ${\displaystyle f}$ ein Maximum und ein Minimum an und es gilt ${\displaystyle f([0,1])\subseteq [\min f,\max f]}$.

Das vorangehende Beispiel ist ein Spezialfall der folgenden Tatsache: Ist ${\displaystyle K}$ ein kompakter topologischer Raum und ${\displaystyle S}$ ein metrischer Raum, so ist jede stetige Abbildung beschränkt. Aufgrund der Stetigkeit existiert zu jedem Punkt ${\displaystyle x\in K}$ ein ${\displaystyle \varepsilon _{x}>0}$, so dass die Inklusion

${\displaystyle f(B_{\varepsilon _{x}}(x))\subset B_{1}(f(x))}$

gilt. Die so definierte offene Überdeckung ${\displaystyle (B_{\varepsilon _{x}}(x))_{x\in K}}$ besitzt aufgrund der Kompaktheit von ${\displaystyle K}$ aber eine endliche Teilüberdeckung mit ${\displaystyle (B_{\varepsilon _{x_{i}}}(x_{i}))_{i=1,\dots ,n}}$ und damit folgt

${\displaystyle f(K)\subset \bigcup _{i=1}^{n}B_{1}(f(x_{i}))}$.

Also ist ${\displaystyle f}$ beschränkt.

Ein Beispiel für e​ine unstetige beschränkte Funktion bildet d​ie Dirichlet-Funktion.

Struktur

Trägt ${\displaystyle S}$ die Struktur eines Vektorraumes, so kann man die Addition und die Skalarmultiplikation in ${\displaystyle B(X;S)}$ punktweise definieren,

${\displaystyle (f+g)(x):=f(x)+g(x)}$ sowie ${\displaystyle (\lambda f)(x):=\lambda f(x){\text{ für alle }}x\in X}$,

wodurch d​ie Menge d​er beschränkten Abbildungen a​uf natürliche Weise z​u einem Vektorraum wird.

Ist ${\displaystyle S}$ ein normierter Raum, so lässt sich eine Norm auf ${\displaystyle B(X;S)}$ erklären durch

${\displaystyle \|f\|_{B(X,S)}:=\sup _{x\in X}\|f(x)\|_{S}}$,

wobei ${\displaystyle \|\cdot \|_{S}}$ die Norm auf ${\displaystyle S}$ bezeichnet. Dies ist genau die Supremumsnorm, sie wird dementsprechend auch mit ${\displaystyle \|\cdot \|_{\infty }}$ oder ${\displaystyle \|\cdot \|_{\operatorname {sup} }}$ bezeichnet, wenn alle beteiligten Räume klar sind.

Ist außerdem ${\displaystyle S}$ ein Banachraum, also vollständig, so ist auch ${\displaystyle B(X;S)}$ ein Banachraum.

Ist ${\displaystyle X}$ ein kompakter Raum, so ist jede stetige Abbildung beschränkt. Es gilt dann die Inklusion

${\displaystyle C(X,S)\subset B(X,S)}$.

Ist ${\displaystyle X}$ kompakt und ${\displaystyle S}$ ein Banachraum, so bilden die stetigen Funktionen einen abgeschlossenen Unterraum der beschränkten Funktionen.

Wichtige Unterräume der beschränkten Abbildungen mit Werten in ${\displaystyle \mathbb {K} }$ sind

• die stetigen Funktionen mit kompaktem Träger ${\displaystyle C_{c}(X)}$,
• die stetigen Funktionen, die im Unendlichen verschwinden ${\displaystyle C_{0}(X)}$ und
• die beschränkten stetigen Funktionen ${\displaystyle C_{b}(X)}$.

Es gelten d​ann die Inklusionen

${\displaystyle B(X)\supset C_{b}(X)\supset C_{0}(X)\supset C_{c}(X)}$.

Literatur

• Hans Wilhelm Alt: Lineare Funktionalanalysis. 6. Auflage. Springer-Verlag, Berlin Heidelberg 2012, ISBN 978-3-642-22260-3, doi:10.1007/978-3-642-22261-0.