Ausflussgeschwindigkeit

Ausflussgeschwindigkeit nennt man die Geschwindigkeit, mit der ein flüssiger oder gasförmiger Körper von sehr niedriger Viskosität (zum Beispiel Wasser) aus einer Öffnung des ihn enthaltenden Gefäßes ausströmt. Da während des Ausströmens eines bestimmten Flüssigkeitsquantums stets eine gleich große Flüssigkeitsmenge von der Oberfläche bis zum Niveau der Öffnung herabsinken muss, so ist die Ausflussgeschwindigkeit gleich der Geschwindigkeit, die ein Körper erlangen würde, wenn er vom Flüssigkeitsspiegel bis zur Ausflussöffnung herabfiele (Torricellis Theorem, siehe auch Bernoulli-Gleichung).

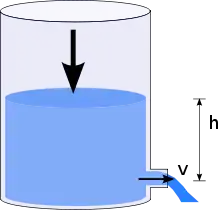
Grafische Darstellung von Torricellis Theorem

Bezeichnet man mit v die Ausflussgeschwindigkeit, mit h die vertikale Tiefe der Öffnung unter der Flüssigkeitsoberfläche (Druckhöhe) und mit g die Schwerebeschleunigung (g = 9,81 ms⁻²), so ist $v={\sqrt {2gh}}$ .

Sie hängt demnach nur von der Druckhöhe, nicht aber von der Dichte der Flüssigkeit ab, so dass z. B. bei gleicher Druckhöhe Wasser und Quecksilber gleich schnell ausfließen.

Da der Druck in einer Flüssigkeit nach allen Richtungen hin gleich stark wirkt, so ist es für die Ausflussgeschwindigkeit gleichgültig, ob sich die Öffnung im Boden oder in einer Seitenwand des Gefäßes befindet, ob der ausfließende Strahl abwärts, seitwärts oder aufwärts (Springbrunnen) gerichtet ist.

Wäre der ausfließende Strahl zylindrisch, so könnte man das pro Zeiteinheit ausgeflossene Flüssigkeitsvolumen leicht berechnen, indem man die Ausflussgeschwindigkeit mit der Fläche der Öffnung multipliziert. Der Strahl ist im Bereich der Ausflussöffnung zylindrisch, wenn die Ausflussöffnung zylindrisch ist. Jedoch gilt die Bernoulli-Gleichung nur in einer stationären Strömung eines reibungsfreien, inkompressiblen Fluids. Daher ist das Ausflussvolumen für reale Flüssigkeiten mit einem Korrekturfaktor zu berechnen. In einiger Entfernung von der Ausflussöffnung ist der Strahl nicht mehr zylindrisch, sondern er zieht sich zusammen, so dass sein Querschnitt in geringer Entfernung von der Öffnung nur noch etwa 61 Prozent von demjenigen der Öffnung beträgt. Um für reale Flüssigkeiten die Ausflussmenge zu erhalten, muss man daher die oben berechnete "theoretische Ausflussmenge" noch mit 0,6 multiplizieren. Diese Zusammenziehung des Strahls (lateinisch contractio venae) rührt hauptsächlich davon her, dass die Flüssigkeitsteilchen im Innern des Gefäßes von allen Seiten her konvergierend zur Öffnung strömen und daher an den Rändern der Abflussöffnung mit einer seitlich gerichteten Geschwindigkeit ankommen.

Alles Bisherige gilt nur für Öffnungen in dünner Gefäßwand. Durch kurze zylindrische oder nach außen konisch erweiterte Ansatzröhren wird, wenn die Flüssigkeit an den Wänden der Röhre adhäriert und diese ganz ausfüllt, die Ausflussmenge vermehrt, die Ausflussgeschwindigkeit dagegen vermindert – auf etwa die Hälfte. Öffnungen in dicker Wand wirken wie Ansatzröhren.

Für die Ausflussgeschwindigkeit idealer Gase gilt ebenfalls das Torricellische Gesetz, wenn man unter der Druckhöhe h die Höhe einer Gassäule von der Dichte des ausströmenden Gases versteht. Bezeichnet man mit h' den manometrisch als Höhe einer Quecksilbersäule gemessenen Überdruck des eingeschlossenen Gases, mit s' das spezifische Gewicht des Quecksilbers, mit s dasjenige des Gases (beide auf Wasser als Einheit bezogen), so verhält sich die Druckhöhe h, die in Rechnung zu bringen ist, zu der Quecksilbersäule h' wie s' zu s; es ist also

h={\frac {h's'}{s}}

und

v={\sqrt {\frac {2gh's'}{s}}}

woraus sich das von Thomas Graham aufgestellte Gesetz ergibt, dass die Ausflussgeschwindigkeiten verschiedener Gase bei gleichem Druck den Quadratwurzeln aus ihren spezifischen Gewichten umgekehrt proportional sind. Da z. B. die Dichte von Wasserstoffgas nur 1/16 der Dichte von Sauerstoffgas beträgt, strömt jenes unter gleichem Druck viermal so schnell aus wie dieses.

Robert Wilhelm Bunsen hat hieraus eine Methode zur Bestimmung der spezifischen Gewichte der Gase abgeleitet.

Quasistationäre Betrachtung des Ausflussgesetzes von Torricelli

Das Ausflussgesetz nach Torricelli erhält man aus der Bernoullischen Energiegleichung. Die vereinfachte Beschreibung der Ausflussgeschwindigkeit $v_{2}$ in Abhängigkeit von der Füllhöhe $h$ unter der Betrachtung, dass der Ausflussdurchmesser viel kleiner ist als der Behälterdurchmesser, lässt sich wie folgt angeben:

v_{2}={\sqrt {2gh}}\qquad \qquad (1)

Dabei ist $g$ die Schwerebeschleunigung ( $g=9{,}81\,{\text{m}}/{\text{s}}^{2}$ ). Nach der Kontinuitätsgleichung der Strömungsdynamik von inkompressiblen Fluiden ist der Volumenstrom ${\dot {V}}$ konstant. Demnach gilt die folgende Formel:

{\dot {V}}=v_{1}A_{1}=v_{2}A_{2}\quad \rightarrow \quad {\frac {v_{1}}{v_{2}}}={\frac {A_{2}}{A_{1}}}={\text{const.}}\qquad \qquad (2)

Wobei $v_{1}$ die Sinkgeschwindigkeit (also die negative Geschwindigkeit) des Wasserpegels $h$ ist. Demnach lässt sich die Formel mit (2) umformulieren zu:

v_{1}={\frac {A_{2}}{A_{1}}}{\sqrt {2gh}}\qquad \qquad (3)

Da nun $v_{1}$ also die negative Geschwindigkeit der Füllhöhe ist, lässt sich dies mit der ersten Ableitung nach der Zeit darstellen. Dadurch erhalten wir eine nichtlineare Differentialgleichung 1. Ordnung, welche nun die Füllhöhe des Behälters über die Zeit beschreibt. Die Differentialgleichung lässt sich wie folgt angeben:

{\frac {\mathrm {d} h}{\mathrm {d} t}}=c{\sqrt {h}}\quad {\text{mit}}\quad c=-{\frac {A_{2}}{A_{1}}}{\sqrt {2g}}\qquad \qquad (4)

Dies ist eine separierbare Differentialgleichung, weshalb sich eine geschlossene Lösung angeben lässt:

\int {\frac {\mathrm {d} h}{\sqrt {h}}}=c\int \mathrm {d} t+C_{1}\quad \rightarrow \quad h(t)={\frac {1}{4}}\left(ct+C_{1}\right)^{2}\quad {\text{mit}}\quad C_{1}\in \mathbb {R} \qquad \qquad (5)

Hierbei ist $C_{1}$ in erster Linie eine beliebige Konstante, welche jedoch durch das Lösen des Anfangswertproblems bestimmt werden kann. Sprich zu Zeitpunkt $t=0\,\mathrm {s}$ hat der Behälter eine Füllhöhe von $h(0)=h_{0}$ . Durch Einsetzen dieser Anfangswerte in die Lösungsfunktion erhält man als Endergebnis:

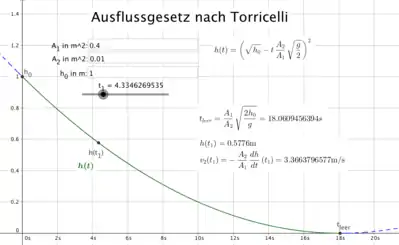
Beispiel zum Verlauf der Funktion h(t)

h(t)=\left({\sqrt {h_{0}}}-t{\frac {A_{2}}{A_{1}}}{\sqrt {\frac {g}{2}}}\right)^{2}={\frac {1}{2}}\left({\frac {A_{2}}{A_{1}}}\right)^{2}gt^{2}-{\sqrt {2gh_{0}}}{\frac {A_{2}}{A_{1}}}t+h_{0}\qquad \qquad (6)

Graphisch betrachtet ist dies eine nach oben geöffnete Parabel, deren Minimum auf der Abszisse liegt und somit eine doppelte Nullstelle ist. Deshalb können wir nun mittels Nullsetzen der erhaltenen Funktion den Zeitpunkt ermitteln zu dem der Behälter leer ist.

{\frac {1}{2}}\left({\frac {A_{2}}{A_{1}}}\right)^{2}gt^{2}-{\sqrt {2gh_{0}}}{\frac {A_{2}}{A_{1}}}t+h_{0}=0\qquad \qquad (7)

Mit ${\tfrac {A_{2}}{A_{1}}}\cdot t_{\text{leer}}=s$ erhalten wir:

{\frac {1}{2}}gs^{2}-{\sqrt {2gh_{0}}}s+h_{0}=0\qquad \qquad (7)

s_{1,2}={\frac {{\sqrt {2gh_{0}}}\pm {\sqrt {2gh_{0}-2gh_{0}}}}{g}}\qquad \qquad (7.1)

s_{1}=s_{2}={\frac {\sqrt {2gh_{0}}}{g}}\qquad \qquad (7.2)

s={\sqrt {\frac {2h_{0}}{g}}}\qquad \qquad (7.3)

{\frac {A_{2}}{A_{1}}}\cdot t_{\text{leer}}={\sqrt {\frac {2h_{0}}{g}}}\qquad \qquad (7.4)

t_{\text{leer}}={\frac {A_{1}}{A_{2}}}{\sqrt {\frac {2h_{0}}{g}}}\qquad \qquad (8)

Alternative Herangehensweise

Alternativ ergibt sich die Ausflussgeschwindigkeit aus der Energieerhaltung von potentieller und kinetischer, spezifischer Energie.

e_{\text{kin}}={\frac {dE_{\text{kin}}}{dV}}={\frac {1}{2}}\rho v_{2}^{2}=\rho gh={\frac {dE_{\text{pot}}}{dV}}=e_{\text{pot}}\quad \rightarrow v_{2}={\sqrt {2gh}}\qquad (8)

Anhand der Kontinuitätsgleichung (2) ergeben sich wiederum Gleichung (3) und (4). Durch erneutes Ableiten von Gleichung (4) nach der Zeit $t$ bietet sich die Möglichkeit die nichtlineare Geschwindigkeitsdifferentialgleichung in eine lineare Beschleunigungsdifferentialgleichung umzuwandeln.

{\frac {{\text{d}}^{2}h}{{\text{d}}t^{2}}}=-{\frac {A_{2}}{A_{1}}}{\sqrt {2g}}{\frac {{\text{d}}{\sqrt {h}}}{{\text{d}}t}}=-{\frac {A_{2}}{A_{1}}}{\sqrt {2g}}{\frac {{\text{d}}{\sqrt {h}}}{{\text{d}}h}}{\frac {{\text{d}}h}{{\text{d}}t}}=\left({\frac {A_{2}}{A_{1}}}\right)^{2}g\quad \rightarrow \quad {\frac {{\text{d}}^{2}h}{{\text{d}}t^{2}}}=\left({\frac {A_{2}}{A_{1}}}\right)^{2}g\qquad (9)

Diese Beschleunigungsdifferentialgleichung (9) lässt sich durch zweifache Integration nach der Zeit t lösen, wodurch sich wiederum Gleichung (6) ergibt. Dabei gelten die Anfangswerte:

{\frac {{\text{d}}h}{{\text{d}}t}}(t=0)=-{\frac {A_{2}}{A_{1}}}{\sqrt {2gh_{0}}},\qquad h(t=0)=h_{0}\qquad (10)

Ausflussbeiwert

Um eine bessere Näherung an den tatsächlich gemessenen Volumenstrom zu erhalten, wird in der Praxis ein Ausflussbeiwert $\mu$ verwendet:

{\dot {V}}_{\text{real}}=\mu \cdot {\dot {V}}_{\text{ideal}}

Der Ausflussbeiwert berücksichtigt sowohl die Verringerung der Ausflussgeschwindigkeit aufgrund des viskosen Verhaltens der Flüssigkeit ("Geschwindigkeitsbeiwert") als auch die Abnahme des effektiven Ausflussquerschnittes aufgrund der vena contracta ("Kontraktionsbeiwert"). Für Flüssigkeiten mit geringer Viskosität (wie bspw. Wasser), die aus einem runden Loch in einem Tank ausströmen, liegt der Ausflussbeiwert in der Größenordnung von 0,65. Durch die Verwendung von ausgerundeten Rohrstutzen kann der Ausflussbeiwert auf über 0,9 erhöht werden[1]. Für rechteckige Öffnungen liegt der Ausflussbeiwert je nach Höhe-Breite-Verhältnis in der Größenordnung zwischen 0,44 und 0,67.

Zudem hängt der Ausflussbeiwert davon ab, ob es sich um eine laminare oder turbulente Strömung handelt. Mit folgender Formel kann dies für Ausströmvorgänge aus einem runden Loch berücksichtigt werden[2]:

$0{,}59+{\frac {5{,}5}{\sqrt {\text{Re}}}}$ mit der Reynolds-Zahl ${\text{Re}}$ .

Einzelnachweise

tec-science: Ausströmen von Flüssigkeiten (Torricelli's Theorem). In: tec-science. 21. November 2019, abgerufen am 8. Dezember 2019.
Hydraulik 9: Ausfluss- und Entleerungszeiten. Abgerufen am 8. Dezember 2019.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] tec-science: Ausströmen von Flüssigkeiten (Torricelli's Theorem). In: tec-science. 21. November 2019, abgerufen am 8. Dezember 2019.

[2] Hydraulik 9: Ausfluss- und Entleerungszeiten. Abgerufen am 8. Dezember 2019.