Aszendent (Astrologie)

Der Aszendent (lat. für ‚das Aufsteigende‘) ist ein Begriff aus der Astrologie. Er ist der Schnittpunkt des Osthorizonts mit der Ekliptik und bezeichnet den zum gegebenen Zeitpunkt und geografischen Ort am östlichen Horizont aufgehenden Grad des Tierkreises. Den gegenüberliegenden Grad am Westhorizont nennt man den Deszendenten (lat. descendere ‚herabsteigen‘).

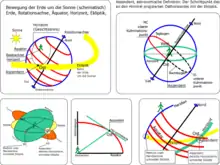
Schematische Darstellung der Position des Aszendenten in 5 Ansichten mit Tagbogen, Meridian/Längengrad, Himmelsmitte, Horizont, Äquator und Ekliptik (Ausschnitt).

Astrologische Definition

Der Aszendent ist der Anfang oder die Spitze des 1. Hauses des zwölfteiligen astrologischen Häuserkreises und gilt als ein sehr wichtiger Faktor im Horoskop. Allgemein beschreibt der Aszendent (unter Einbeziehung anderer Deutungselemente) nach Ansicht von vielen Astrologen auch die Persönlichkeit oder zumindest einen entscheidenden Anteil davon. Vom Aszendenten als Ausgangspunkt sollen sich Hinweise auf die Grundmotivation, mit der der Horoskopeigner ins Leben tritt, ermitteln lassen. Er soll beispielsweise anzeigen, mit welchem instinktiven Temperament und zunächst unbewussten 'Lebenskräften' der Geborene im Kern ausgestattet ist.[1] Traditionellere Sichtweisen verbinden mit dem Aszendenten den Körperbau und Lebensvitalität.[2] In astrologischen Richtungen, die mit den so genannten Halbsummen arbeiten, soll der Aszendent abbilden, wie der Mensch auf seine Mitwelt wirkt, wie er von ihr gesehen und wahrgenommen wird. Er symbolisiert dabei den Einfluss anderer auf das eigene Verhalten sowie die eigene Reaktion auf die Umwelt.[3]

Berechnung des Aszendenten

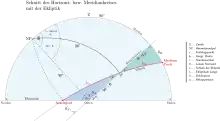
Zusammenhänge zwischen Aszendent, Horizont und Himmelsäquator

Um das Tierkreiszeichen des Schnittpunktes von Horizont und Ekliptik bei gegebener lokaler Sternzeit θ, geografischer Breite Φ und der Schiefe der Ekliptik ε = 23° 26′ 21,45″ (J2000.0) bestimmen zu können, muss dessen ekliptikale Länge λ bestimmt werden. Aus dem Dreieck der Großkreise Horizont (im astronomischen Sinn), Himmelsäquator und Ekliptik auf der Himmelskugel (siehe Grafik) ergibt sich nach dem Kotangenssatz folgender Zusammenhang:

\sin \epsilon \cdot \cot \left({\pi /2+\phi }\right)=\sin \left({\pi /2+\theta }\right)\cdot \cot \left(\lambda \right)-\cos \left({\pi /2+\theta }\right)\cdot \cos \epsilon

Aus $\cot(\pi /2+\phi )=-\tan \phi \,,\,\,\sin(\pi /2+\theta )=\cos \theta \,,\,\,\cos(\pi /2+\phi )=-\sin \phi$ folgt:

\tan \lambda ={\frac {-\cos \theta }{\sin \theta \cos \epsilon +\tan \phi \sin \epsilon }}

Da die meisten Implementierungen der Arkustangens Funktion den Wertebereich $(-\pi /2;\pi /2)$ besitzen, muss der zurückgegebene Wert noch durch λ mod 180° umgerechnet werden. Des Weiteren gibt es zwei Schnittpunkte zwischen Horizont und Ekliptik. Um festzustellen, welchen Punkt Arkustangens zurückgibt, betrachtet man den Quadranten von θ. Gilt $\pi /2<\theta <3\pi /2$ wird der Deszendent zurückgegeben, ansonsten der Aszendent.

Zur Umrechnung zwischen Aszendenten und Deszendenten addiert man 180° und bringt ggf. das Ergebnis – zum Beispiel mit (λ + 180°) mod 360 – wieder in den Wertebereich $(0;2\pi )$ .

Bestimmen des Tierkreiszeichens

Die in der Astrologie verwendeten zwölf Tierkreiszeichen teilen die Ekliptik in 30°-Schritten. Mittels der berechneten ekliptikalen Länge λ kann durch die Tabelle der Tierkreiszeichen das entsprechende Tierkreiszeichen ermittelt werden.

Durch den Präzessionseffekt bewegt sich die Basis des ekliptikalen Koordinatensystems – der Frühlingspunkt – auf der Ekliptik weiter. Dadurch ändert sich die Lage aller Fixsterne und somit auch der Sternbilder im tropischen Tierkreis. Insofern unterscheidet sich das heutige astronomische Sternbild des Aszendenten vom astrologischen.

Deklination und Rektaszension des Aszendenten

Da β = 0° (ekliptikale Breite) ist die Umrechnung von ekliptikalen und äquatorialen Koordinaten besonders einfach: es gilt sin ε · sin λ = sin δ und tan λ · cos ε = tan α.

Spezialfälle

An den Polen schneidet der Frühlingspunkt stets den Horizont. Der Aszendent hat daher je nach Tageszeit immer die ekliptikale Länge 0° oder 180°.
An den Polarkreisen ist einmal am Tag die Horizontebene parallel mit der Ekliptikebene (bei θ = 90° am südlichen und θ = 270° am nördlichen Polarkreis). Die beiden Großkreise fallen dann zusammen und es kann kein Aszendent definiert werden.

Abschätzen des Fehlers

Da θ, Φ und ε stets fehlerbehaftete Größen sind, kann der Fehler durch das totale Differential $\Delta \lambda =\left|{\frac {\partial \lambda }{\partial \theta }}\right|\Delta \theta +\left|{\frac {\partial \lambda }{\partial \phi }}\right|\Delta \phi +\left|{\frac {\partial \lambda }{\partial \varepsilon }}\right|\Delta \varepsilon$ abgeschätzt werden. Der maximale Fehler lässt sich durch das Maximieren der partiellen Ableitungen errechnen; dies ist jedoch nicht sinnvoll, da die Funktion wie bei den Spezialfällen erwähnt am Polarkreis eine Polstelle besitzt und der Fehler dort theoretisch unendlich groß sein würde.

Sinnvoller ist eine statistische Methode: für 99 % aller Werte ist der Fehler besser als $\Delta \lambda =2,77\Delta \theta +6,42\Delta \phi +6,25\Delta \epsilon$

Dies bedeutet, dass bei 99 % aller möglichen Werte für θ, Φ und ε die partiellen Ableitungen kleiner sind als die dargestellten Zahlen. Da sich die lokale Sternzeit durch Addition der geografischen Länge zur Sternzeit am Nullmeridian errechnet, kann auch $\Delta \theta =\Delta \Theta +\Delta l$ geschrieben werden.

Daraus lässt sich erkennen, dass für eine Bestimmung von λ mit einer Genauigkeit von 1° die geografische Breite des Geburtsortes mindestens auf 9' genau bekannt sein muss, dies entspricht rund 17 km für den 50. Breitengrad. Die Geburtszeit geht additiv in die Sternzeit ein, der erlaubte Fehler ist 1°/2.77, dies entspricht einem Zeitraum von ca. 1,5 Minuten und ist die erforderliche Genauigkeit der Geburtszeit.

Zur Bestimmung des jeweiligen Tierkreiszeichens ist (je nach Ort und Zeit) eine deutlich größere Ungenauigkeit zulässig. Für den 18. Februar 1983 ist für ganz Deutschland von 11:00 Uhr bis 11:40 Uhr der Aszendent Zwilling, an einzelnen Orten in Deutschland beginnt der Aszendent jeweils zwischen 10:00 Uhr (im Nordosten) und 11:00 Uhr und endet nach 1,5 Stunden bis 2 Stunden zwischen 11:40 Uhr und 12:45 Uhr (im Südwesten).

Beispiele

Breite [°]	Länge [°]	Datum (UT)	JD	T	Θ [°]	θ [°]	tan(λ)	S₁ [°]	S₂ [°]	Aszendent	Position [°]
48	16	10.11.1983 13:04	2445649,04444	-0,161422466	-2128074,8724	261,1276	-0,331882633	161,6399	341,6399	Fische	11,6399
-61	-27	10.12.1986 23:12	2446775,46667	-0,130582706	-1721452,6173	40,3827	6,183809507	80,8141	260,8141	Zwillinge	20,8141
78	17	07.08.2007 13:08	2454320,04722	0,075976652	1002032,6786	169,6786	0,483263665	25,7928	205,7928	Waage	25,7928
-30	161	16.12.2002 23:32	2452625,48056	0,029581945	390318,4334	239,4334	-0,498741575	153,4927	333,4927	Fische	3,4927
17	57	17.05.1987 18:18	2446933,26250	-0,126262491	-1664490,5863	206,4137	-3,125708396	107,7409	287,7409	Steinbock	17,7409
-1	-58	18.09.1979 03:35	2444134,64931	-0,202884345	-2674749,7820	352,2180	7,553238471	82,4583	262,4583	Zwillinge	22,4583
63	-17	17.09.1987 01:24	2447055,55833	-0,122914214	-1620343,5457	359,4543	-1,295373592	127,6674	307,6674	Löwe	7,6674
-14	-6	06.12.2020 00:27	2459189,51875	0,209295517	2759842,0104	76,0104	-0,305584898	163,0076	343,0076	Jungfrau	13,0076
-17	-61	28.10.1976 14:19	2443080,09653	-0,231756426	-3055428,1992	190,8008	-3,346284094	106,6382	286,6382	Steinbock	16,6382
-27	51	03.09.2010 02:04	2455442,58611	0,106710092	1407253,1061	64,1061	-0,701318031	144,9573	324,9573	Löwe	24,9573
45	-93	03.08.2008 09:41	2454681,90347	0,085883736	1132657,5913	4,5913	-2,115346746	115,3018	295,3018	Krebs	25,3018
-90	-21	25.05.2015 07:15	2457167,80208	0,153943931	2030031,3107	330,3107	0,000000000	0,0000	180,0000	Widder	0,0000
-36	20	21.11.1987 12:15	2447121,01042	-0,121122234	-1596716,2831	263,7169	-0,091126331	174,7932	354,7932	Fische	24,7932
-3	-178	12.07.2016 19:13	2457582,30069	0,165292285	2179659,3601	41,3601	-1,282114641	127,9529	307,9529	Löwe	7,9529

Legende: Breite/Länge: Breiten bzw. Längengrade, nach Süden bzw. Westen negativ; JD: Julianisches Datum; T: Julianische Jahrhunderte seit J2000.0; Θ: Sternzeit am Nullmeridian; θ: lokale Sternzeit; S₁ bzw. S₂: Schnittpunkte der Ekliptik mit dem Horizont; Position: Längendifferenz zum Sternzeichenbeginn

Weblinks

Wiktionary: Aszendent – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Nicolaus Klein: Arbeitsbuch zur Astrologie. Heinrich Hugendubel Verlag, München 1993. S. 39f.
William Lilly: Christliche Astrologie. Buch 1 und Buch 2. Chiron Verlag, Tübingen 2007. S. 70f.
Reinhold Ebertin: Die Kombination der Gestirneinflüsse. Ebertin Verlag, Freiburg /Breisgau 1983. S. 76f.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Nicolaus Klein: Arbeitsbuch zur Astrologie. Heinrich Hugendubel Verlag, München 1993. S. 39f.

[2] William Lilly: Christliche Astrologie. Buch 1 und Buch 2. Chiron Verlag, Tübingen 2007. S. 70f.

[3] Reinhold Ebertin: Die Kombination der Gestirneinflüsse. Ebertin Verlag, Freiburg /Breisgau 1983. S. 76f.