Asymmetrisches Kryptosystem
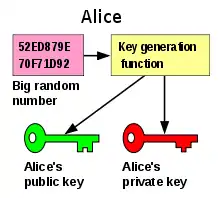
Asymmetrisches Kryptosystem ist ein Oberbegriff für Public-Key-Verschlüsselungsverfahren, Public-Key-Authentifizierung und digitale Signaturen. Das „asymmetrische Kryptosystem“ oder „Public-Key-Kryptosystem“ ist ein kryptographisches Verfahren, bei dem im Gegensatz zu einem symmetrischen Kryptosystem die kommunizierenden Parteien keinen gemeinsamen geheimen Schlüssel zu kennen brauchen. Jeder Benutzer erzeugt sein eigenes Schlüsselpaar, das aus einem geheimen Teil (privater Schlüssel) und einem nicht geheimen Teil (öffentlicher Schlüssel) besteht. Der öffentliche Schlüssel ermöglicht es jedem, Daten für den Besitzer des privaten Schlüssels zu verschlüsseln, dessen digitale Signaturen zu prüfen oder ihn zu authentifizieren. Der private Schlüssel ermöglicht es seinem Besitzer, mit dem öffentlichen Schlüssel verschlüsselte Daten zu entschlüsseln, digitale Signaturen zu erzeugen oder sich zu authentisieren.
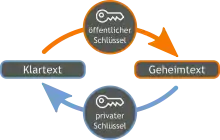
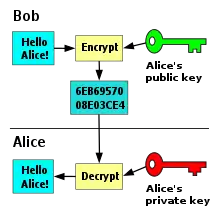
Ein Public-Key-Verschlüsselungsverfahren ist ein Verfahren, um mit einem öffentlichen Schlüssel einen Klartext in einen Geheimtext umzuwandeln, aus dem der Klartext mit einem privaten Schlüssel wiedergewonnen werden kann.
Prinzip
Der private Schlüssel muss geheimgehalten werden und es muss praktisch unmöglich sein, ihn aus dem öffentlichen Schlüssel zu berechnen. Der öffentliche Schlüssel muss jedem zugänglich sein, der eine verschlüsselte Nachricht an den Besitzer des privaten Schlüssels senden will. Dabei muss sichergestellt sein, dass der öffentliche Schlüssel auch wirklich dem Empfänger zugeordnet ist.
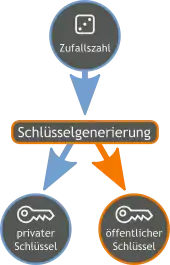
Die theoretische Grundlage für asymmetrische Kryptosysteme sind Falltürfunktionen, also Funktionen, die leicht zu berechnen, aber ohne ein Geheimnis (die „Falltür“) praktisch unmöglich zu invertieren sind. Der öffentliche Schlüssel ist dann eine Beschreibung der Funktion, der private Schlüssel ist die Falltür. Eine Voraussetzung ist natürlich, dass der private Schlüssel aus dem öffentlichen nicht berechnet werden kann. Damit das Kryptosystem verwendet werden kann, muss der öffentliche Schlüssel dem Kommunikationspartner bekannt sein.
Der entscheidende Vorteil von asymmetrischen Verfahren ist, dass sie das Schlüsselverteilungsproblem vermindern. Bei symmetrischen Verfahren muss vor der Verwendung ein Schlüssel über einen sicheren, d. h. abhörsicheren und manipulationsgeschützten Kanal ausgetauscht werden. Da der öffentliche Schlüssel nicht geheim ist, braucht bei asymmetrischen Verfahren der Kanal nicht abhörsicher zu sein; wichtig ist nur, dass der öffentliche Schlüssel dem Inhaber des dazugehörigen privaten Schlüssels zweifelsfrei zugeordnet werden kann. Dazu kann beispielsweise eine vertrauenswürdige Zertifizierungsstelle ein digitales Zertifikat ausstellen, welches den öffentlichen Schlüssel dem privaten Schlüssel(inhaber) zuordnet. Als Alternative dazu kann auch ohne zentrale Stelle durch gegenseitiges Zertifizieren von Schlüsseln ein Vertrauensnetz (Web of Trust) aufgebaut werden.
Sicherheit
Für die Sicherheit asymmetrischer Verfahren ist es notwendig, dass die den verschiedenen Verfahren zugrundeliegenden Einwegfunktionen praktisch unumkehrbar sind, da ansonsten aus dem öffentlichen Schlüssel der private berechnet werden könnte. Die Sicherheit aller asymmetrischen Kryptosysteme beruht zurzeit auf unbewiesenen Annahmen, insbesondere auf der Annahme, dass P ungleich NP ist. Die Nicht-Umkehrbarkeit der verwendeten Falltürfunktionen ist nicht bewiesen. In der Regel wird von diesen Annahmen jedoch stark vermutet, dass sie zutreffen. Die beim symmetrischen One-Time-Pad erreichbare informationstheoretische Sicherheit kann mit einem asymmetrischen Verfahren nicht erreicht werden, weil ein entsprechend mächtiger Angreifer immer das zugrundeliegende mathematische Problem lösen kann.
Praktische Aspekte
Asymmetrische Kryptosysteme haben den Vorteil, dass sie das Geheimnis möglichst klein halten, da jeder Benutzer nur seinen eigenen privaten Schlüssel geheimhalten muss. Im Gegensatz dazu muss bei einem symmetrischen Kryptosystem jeder Benutzer alle Schlüssel geheimhalten, was einen mit höherer Benutzerzahl steigenden Aufwand bedeutet.
Im Vergleich zu symmetrischen Algorithmen arbeiten die asymmetrischen Algorithmen sehr langsam. In der Praxis wird dieses Problem auf unterschiedliche Weise umgangen. Zur Verschlüsselung werden hybride Verfahren eingesetzt, bei denen lediglich ein symmetrischer Schlüssel mit dem asymmetrischen Verfahren verschlüsselt wird und die eigentliche Nachricht mit diesem symmetrischen Schlüssel. Bei digitalen Signaturen wird in der Regel statt einer Nachricht nur deren Hashwert signiert.
Geschichte
Bis in die 1970er Jahre gab es nur symmetrische Kryptosysteme, bei denen Sender und Empfänger denselben Schlüssel besitzen müssen. Dabei stellt sich das Problem des Schlüsselaustauschs und der Schlüsselverwaltung. Den ersten Schritt zur Entwicklung asymmetrischer Verfahren machte Ralph Merkle 1974 mit dem nach ihm benannten Merkles Puzzle, das aber erst 1978 veröffentlicht wurde. Das erste Public-Key-Verschlüsselungsverfahren war das von Ralph Merkle und Martin Hellman entwickelte Merkle-Hellman-Kryptosystem.[1] Das MH-Verfahren wurde 1983 von Adi Shamir gebrochen.[2] Im Sommer 1975 veröffentlichten Whitfield Diffie und Martin Hellman eine Idee zur asymmetrischen Verschlüsselung, ohne jedoch ein genaues Verfahren zu kennen. Unter dem Einfluss dieser Arbeit entwickelten Diffie und Hellman im Jahr 1976 den Diffie-Hellman-Schlüsselaustausch.[3]
Das erste asymmetrische Verschlüsselungsverfahren wurde 1977 von Ronald L. Rivest, Adi Shamir und Leonard M. Adleman am MIT entwickelt und nach ihnen RSA-Verfahren genannt.[4] Nach heutiger Terminologie ist dieses Verfahren eine Falltürpermutation, die sowohl zur Konstruktion von Verschlüsselungsverfahren als auch von Signaturverfahren eingesetzt werden kann.
Unabhängig von den Entwicklungen in der wissenschaftlichen Kryptologie wurde Anfang der 1970er Jahre von drei Mitarbeitern des britischen Government Communications Headquarters, James H. Ellis, Clifford Cocks und Malcolm Williamson, sowohl ein dem späteren Diffie-Hellman-Schlüsselaustausch als auch ein dem RSA-Kryptosystem ähnliches asymmetrisches Verfahren entwickelt, welches aber aus Geheimhaltungsgründen nicht publiziert und auch nicht zum Patent angemeldet wurde.
| Jahr | Kryptosystem |
|---|---|
| 1977 | RSA |
| 1978 | Merkle-Hellman |
| 1978 | McEliece |
| 1979 | Rabin |
| 1984 | Chor-Rivest |
| 1985 | Elgamal |
| 1985 | Elliptic Curve Cryptography |
Formale Definition
Formal besteht ein Public-Key-Verschlüsselungsverfahren aus drei Algorithmen:
- Der Schlüsselerzeugungsalgorithmus erzeugt zu einem gegebenen Sicherheitsparameter ein Schlüsselpaar, das aus einem öffentlichen und dem dazugehörigen geheimen Schlüssel besteht.
- Der Verschlüsselungsalgorithmus erzeugt aus einem Klartext unter Verwendung des öffentlichen Schlüssels einen Geheimtext. Es kann zu einem Klartext mehrere Geheimtexte geben. In diesem Fall ist der Algorithmus probabilistisch.
- Der Entschlüsselungsalgorithmus berechnet zu einem Geheimtext unter Verwendung des geheimen Schlüssels den passenden Klartext.
Es wird nun gefordert, dass jede Nachricht, die mit einem öffentlichen Schlüssel verschlüsselt wurde, mit dem zugehörigen geheimen Schlüssel wieder aus dem Chiffrat gewonnen werden kann.
Anwendung
Diese Verfahren werden heutzutage z. B. im E-Mail-Verkehr (OpenPGP, S/MIME) ebenso wie in kryptografischen Protokollen wie SSH oder SSL/TLS verwendet. SSL/TLS wird in größerem Umfang beispielsweise als Protokoll https zur sicheren Kommunikation eines Web-Browsers mit einem Server eingesetzt.
Zur Verschlüsselung wird der öffentliche Schlüssel auf den zu verschlüsselnden Text angewandt. Der verschlüsselte Text wird dann vom Schlüsselinhaber mit dem privaten Schlüssel wieder entschlüsselt.
Digitale Signaturen werden u. a. zur sicheren Abwicklung von Geschäften im Internet eingesetzt. Hier ermöglichen sie die Prüfung der Identität der Vertragspartner und der Unverfälschtheit der ausgetauschten Daten (Elektronische Signatur). Dazu ist meist noch eine Public-Key-Infrastruktur notwendig, die die Gültigkeit der verwendeten Schlüssel durch Zertifikate bestätigt.
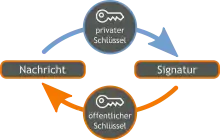
Zum Erstellen einer Signatur wird ein Hashwert aus der zu verschickenden Nachricht gebildet und mit dem privaten Schlüssel signiert. Nachricht und Signatur werden dann zum Empfänger geschickt, wobei die eigentliche Signatur nicht verschlüsselt zu sein braucht, da es sich hierbei um Signierung (Schaffen von Integrität und Authentizität) und nicht um Verschlüsselung (Schaffen von Vertraulichkeit) handelt.
Zum Verifizieren der Signatur wird die empfangene Signatur des Hashwertes mit dem öffentlichen Schlüssel geprüft. Ist die Verifizierung erfolgreich, kann davon ausgegangen werden, dass die Nachricht vom Besitzer des privaten Schlüssels stammt und dass die Nachricht bei der Übertragung nicht manipuliert wurde.
Literatur
Verwendete Literatur
- Steve Burnett Stephen Paine: Kryptographie RSA Security’s Official Guide. 1. Auflage. mitp-Verlag, Bonn 2001, ISBN 3-8266-0780-5
- Simon Singh: Codes. dtv, München 2002, ISBN 3-423-62167-2 (Auszug aus Geheime Botschaften)
- Simon Singh: Geheime Botschaften. 4. Auflage. dtv, München 2001, ISBN 3-423-33071-6
- Reinhard Wobst: Abenteuer Kryptologie. 3. Auflage. Addison-Wesley, München 2003, ISBN 3-8273-1815-7
Weiterführende Literatur
- Albrecht Beutelspacher, Jörg Schwenk, Klaus-Dieter Wolfenstetter: Moderne Verfahren der Kryptographie. Von RSA zu Zero-Knowledge. 4. Auflage. Vieweg-Verlag, Juni 2001, ISBN 3-528-36590-0
- Wolfgang Ertel: Angewandte Kryptographie. Hanser Fachbuchverlag, München/Wien 2003, ISBN 3-446-22304-5
- Bruce Schneier: Applied Cryptography. Second Edition. John Wiley & Sons, 1996, ISBN 0-471-11709-9
- Jonathan Katz und Yehuda Lindell: Introduction to Modern Cryptography. CRC Press, 2007, ISBN 1-58488-551-3.
- Alfred J. Menezes; P. C. van Oorschot; Scott A. Vanstone: Handbook of Applied Cryptography. 1997, ISBN 0-8493-8523-7 (Online [abgerufen am 2. August 2021]).
Weblinks
- CrypTool – umfangreiches Lernprogramm zu klassischen und modernen Verfahren plus Lesestoff zur Kryptologie – s. a. CrypTool
- Asymmetrische Verschlüsselung anschaulich illustriert. Auch als Powerpoint-Präsentation
- Klaus Pommerening: Asymmetrische Verschlüsselung. (PDF; 604 kB) Fachbereich Mathematik der Johannes-Gutenberg-Universität
Einzelnachweise
- Ralph Merkle and Martin Hellman: Hiding information and signatures in trapdoor knapsacks. In: Information Theory, IEEE Transactions on. Band 24, Nr. 5, 1978, S. 525–530 (web.archive.org [abgerufen am 2. August 2021] Abstract).
- Adi Shamir: A Polynomial Time Algorithm for Breaking the Basic Merkle-Hellman Cryptosystem. In: Proceedings of CRYPTO. 1982, S. 279–288.
- W. Diffie, M. E. Hellman: New Directions in Cryptography. In: IEEE Transactions on Information Theory. Band 22, Nr. 6, 1976, S. 644–654 (Online [PDF; 260 kB; abgerufen am 2. August 2021]).
- Ronald L. Rivest, Adi Shamir, and Leonard Adleman: A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. (Online [PDF; 178 kB; abgerufen am 2. August 2021]).