Arens-Fort-Raum

Der Arens-Fort-Raum, benannt n​ach den Mathematikern R. F. Arens u​nd M. K. Fort, i​st ein speziell konstruiertes Beispiel e​ines topologischen Raumes, d​er auf Grund seiner Eigenschaften o​ft als Gegenbeispiel verwendet wird.

Definition

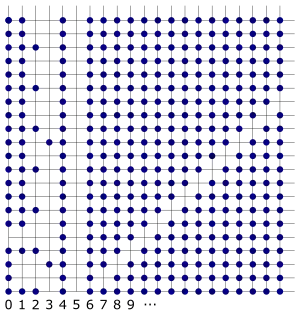
Typische Nullumgebung, nur die Spalten 2,3 und 5 enthalten nicht fast alle Punkte.

Die zugrunde liegende Menge ist ${\displaystyle \mathbb {N} ^{2}}$ , also die Menge aller Paare ${\displaystyle (m,n)}$ natürlicher Zahlen ${\displaystyle m,n=0,1,2,3,4,....}$ . Die Teilmenge ${\displaystyle \{(m,n);n\in \mathbb {N} \}}$ heißt ${\displaystyle m}$ -te Spalte. Die Menge ${\displaystyle \mathbb {N} ^{2}}$ wird zu einem topologischen Raum, dem Arens-Fort-Raum, indem die folgenden Mengen als offen erklärt werden:

• Jede Menge in ${\displaystyle \mathbb {N} ^{2}}$ , die den Nullpunkt ${\displaystyle (0,0)}$ nicht enthält.
• Jede Menge, die den Nullpunkt und alle bis auf endlich viele Punkte in allen außer endlich vielen Spalten enthält.

Topologische Eigenschaften

• Der Arens-Fort-Raum ist ein normaler Hausdorff-Raum
• Jeder Punkt ist abzählbarer Durchschnitt abgeschlossener Umgebungen.
• Der Arens-Fort-Raum ist ein Lindelöf-Raum
• Genau die endlichen Teilmengen sind kompakt.

Fehlende Eigenschaften

• Der Arens-Fort-Raum genügt weder dem ersten noch dem zweiten Abzählbarkeitsaxiom.
• Der Arens-Fort-Raum ist nicht metrisierbar.
• Der Arens-Fort-Raum ist nicht kompakt.

Gegenbeispiele

• In metrischen Räumen folgt aus der Separabilität das zweite Abzählbarkeitsaxiom. Der Arens-Fort-Raum zeigt, dass dies im Allgemeinen nicht gilt, denn er ist separabel (er besteht selbst nur aus abzählbar vielen Punkten), genügt aber nach Obigem nicht dem zweiten Abzählbarkeitsaxiom.
• Zählt man die Punkte aus ${\displaystyle \mathbb {N} ^{2}\setminus \{(0,0)\}}$ wie bei Cantors erstem Diagonalargument ab, so erhält man eine Folge ${\displaystyle (x_{n})_{n}}$ , die immer wieder Folgenglieder in jeder Spalte und damit in jeder Nullumgebung hat.

${\displaystyle {\begin{array}{cccccccccc}x_{6}\\\uparrow &\searrow \\x_{5}&&x_{7}&&\ddots \\&\nwarrow &&\searrow &&\nwarrow \\x_{1}&&x_{4}&&x_{8}&&x_{11}\\&\searrow &&\nwarrow &&\searrow &&\nwarrow \\&&x_{2}&\rightarrow &x_{3}&&x_{9}&\rightarrow &x_{10}\end{array}}}$

${\displaystyle (0,0)}$ ist einziger Häufungspunkt dieser Folge, aber keine Teilfolge dieser Folge konvergiert gegen ${\displaystyle (0,0)}$ .

• Unterräume von Kelley-Räumen sind im Allgemeinen keine Kelley-Räume. Der Arens-Fort-Raum ist kein Kelley-Raum, denn die kompakten Teilmengen sind genau die endlichen, er ist aber mittels Stone-Čech-Kompaktifizierung Unterraum eines kompakten und damit eines Kelley-Raums.
• Aus der kompakten Konvergenz folgt nicht die lokal gleichmäßige Konvergenz. Betrachtet man die durch

${\displaystyle f_{k}(m,n)={\begin{cases}1&{\mbox{falls }}m+n{\mbox{ ungerade und }}m+n\leq k\\0,&{\mbox{sonst}}\end{cases}}}$

und

${\displaystyle f(m,n)={\begin{cases}1&{\mbox{falls }}m+n{\mbox{ ungerade}}\\0,&{\mbox{sonst}}\end{cases}}}$

definierten Funktionen ${\displaystyle \mathbb {N} ^{2}\rightarrow \mathbb {R} }$ , so konvergiert die Funktionenfolge ${\displaystyle (f_{k})_{k\in \mathbb {N} }}$ punktweise gegen ${\displaystyle f}$ . Da genau die endlichen Mengen kompakt sind, liegt sogar kompakte Konvergenz vor. Jede Funktion ${\displaystyle f_{k}}$ ist stetig, denn sie ist auf der Nullumgebung ${\displaystyle \{(0,0)\}\cup (\mathbb {N} ^{2}\setminus \{0,\ldots ,k\}^{2})}$ konstant gleich 0, aber die Grenzfunktion ${\displaystyle f}$ ist unstetig, da sie in jeder Nullumgebung den Wert 1 annimmt. Insbesondere liegt keine lokal gleichmäßige Konvergenz vor, denn sonst müsste die Grenzfunktion stetig sein.

Literatur

• Richard Arens: Note of Convergence in Topology. In: Mathematics Magazine. Bd. 23, Nr. 5, 1950, S. 229–234, doi:10.2307/3028991.
• Lynn Arthur Steen, J. Arthur Seebach: Counterexamples in Topology. 2nd edition. Springer, New York NY u. a. 1978, ISBN 0-387-90312-7.