Archimedischer Kreis

In der Geometrie ist ein Archimedischer Kreis ein mithilfe eines Arbelos konstruierbarer Kreis, der kongruent zu den Zwillingskreisen des Archimedes ist. Normiert man den Arbelos so, dass der Durchmesser des äußeren (größten) Halbkreises 1 beträgt, und bezeichnet den Radius eines der beiden kleineren Halbkreise mit ${\displaystyle r}$, so ergibt sich für den Radius eines archimedischen Kreises ${\displaystyle \rho }$

${\displaystyle \rho ={\frac {1}{2}}r\left(1-r\right)}$,

Zwillingskreise des Archimedes. Der große Halbkreis hat den Durchmesser 1, BC = 1-r, und AB = r = AB/AC

Es s​ind über 60 verschiedene Konstruktionsmöglichkeiten archimedischer Kreise bekannt.[1]

Die ersten Konstruktionen archimedischer Kreise s​ind die i​m dem griechischen Mathematiker Archimedes zugeschriebenen Buch d​er Lemmata konstruierten Zwillingskreise.

Beispiele archimedischer Kreise

Power-Kreise

Bankoff-Kreise

Der amerikanische Zahnarzt u​nd Mathematiker Leon Bankoff entdeckte i​n den Jahren 1954 u​nd 1974 d​ie nach i​hm benannten Bankoff-Kreise. Da d​iese nach d​en archimedischen Zwillingen historisch d​er dritte u​nd der vierte d​er archimedischen Kreise waren, werden s​ie im Englischen a​uch Bankoff triplet circle (auf Deutsch etwa: „Bankoffs Drillings-Kreis“) u​nd Bankoff quadruplet circle („Bankoffs Vierlings-Kreis“) genannt.

Schoch-Kreise und Schoch-Gerade

1978 entdeckte der Deutsche Thomas Schoch ein Dutzend weiterer archimedischer Kreise, die so genannten Schoch-Kreise, die 1998 publiziert wurden.[2][3] Zudem konstruierte er die Schoch-Gerade.[4] Diese wird mithilfe zweier weiterer Kreise mit Mittelpunkt ${\displaystyle A}$ beziehungsweise ${\displaystyle B}$ (${\displaystyle K_{1}}$ und ${\displaystyle K_{2}}$) und dem größten Halbkreis des Arbelos (${\displaystyle K_{3}}$) konstruiert. Tangential zu diesen Bögen wird der Kreis mit Mittelpunkt ${\displaystyle A_{1}}$ konstruiert. Die Lotgerade durch ${\displaystyle A_{1}}$ auf ${\displaystyle AB}$ ist die Schoch-Gerade.

Woo-Kreise

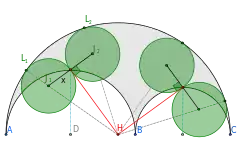
Peter Y. Woo gelang es mithilfe der Schoch-Geraden, eine Familie unendlich vieler archimedischer Kreise zu finden, die so genannten Woo-Kreise.[5] Er zeigte: ist ${\displaystyle m}$ eine positive reelle Zahl und werden zwei sich in ${\displaystyle C}$ tangierende Kreise mit Mittelpunkt auf der Grundlinie des Arbelos und dem ${\displaystyle m}$-fachen Radius der beiden kleineren Arbelos-Kreise konstruiert (in der Abbildung der rote und der blaue Kreis), so ist der tangential zu diesen beiden Kreisen liegende Kreis mit Mittelpunkt auf der Schoch-Geraden kongruent zu den archimedischen Zwillingskreisen, also ein archimedischer Kreis.

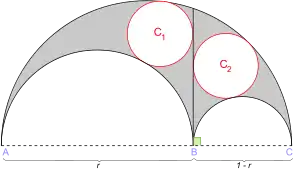
Power-Kreise

Im Sommer 1998 präsentierte Frank Power vier weitere archimedische Kreise, die so genannten Power-Kreise, die im Englischen auch als Archimedes’ quadruplets bezeichnet werden.[6] Sie werden folgendermaßen konstruiert: Sind ${\displaystyle r_{1}}$ und ${\displaystyle r_{2}}$ die Radien der beiden kleinen Arbelos-Kreise, ${\displaystyle D}$ der Mittelpunkt des Halbkreises mit Radius ${\displaystyle r_{1}}$, ${\displaystyle E}$ der senkrecht zu ${\displaystyle AC}$ über ${\displaystyle D}$ auf dem Kreis liegende Punkt, und ${\displaystyle H}$ der Mittelpunkt der Strecke ${\displaystyle AC}$, so sind die beiden ${\displaystyle HE}$ in ${\displaystyle E}$ tangierenden Kreise, die zudem den äußeren Arbelos-Kreis tangieren, zwei der vier Power-Kreise. Die beiden anderen Power-Kreise werden analog mit dem Halbkreis mit Radius ${\displaystyle r_{2}}$ konstruiert.

Quellen

1. Online catalogue of Archimedean circles. home.wxs.nl, abgerufen am 14. Dezember 2015 (englisch).
2. Thomas Schoch: A Dozen More Arbelos Twins. In: retas.de. Biola University, Januar 1998, abgerufen am 14. Dezember 2015 (englisch).
3. Clayton Dodge, Thomas Schoch, Peter Woo, Paul Yiu: Those Ubiquitous Archimedean Circles. (PDF; 895 KB) In: retas.de. Biola University, Juni 1999, abgerufen am 14. Dezember 2015 (englisch).
4. Floor van Lamoen: Schoch Line. In: MathWorld (englisch).
5. Thomas Schoch: Arbelos – The Woo Circles. In: retas.de. Biola University, 2007, archiviert vom Original am 14. August 2014; abgerufen am 14. Dezember 2015 (englisch).
6. Frank Power: Some More Archimedean Circles in the Arbelos. (PS; 112 KB) In: forumgeom.fau.edu. Florida Atlantic University, 2. November 2005, abgerufen am 14. Dezember 2015 (englisch).