Apothema

Das Apothema (altgriechisch ἀπόθεμα ‚Ablage‘) einer Kreissehne ist ihr Abstand vom Mittelpunkt des Kreises, also die Länge des Lotes vom Mittelpunkt auf die Sehne.[1]

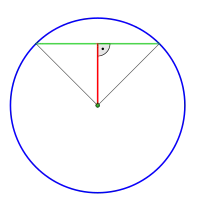
Das Apothema eines regelmäßigen Vielecks[2] ist das Apothema seiner Kanten (als Sehnen im Umkreis) und gleichzeitig sein Inkreisradius.

Berechnung

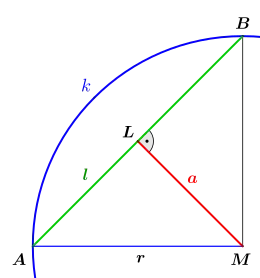
Apothema der Sehne AB (mit Mittelpunkt L) eines Kreises (um M) ist die Länge a = ML.

Ist $r$ der Kreisradius und $l$ die Länge der Kreissehne, dann gilt nach dem Satz des Pythagoras für das Apothemas $a$

r^{2}=a^{2}+{\frac {l^{2}}{4}}

und damit

a={\sqrt {r^{2}-{\tfrac {l^{2}}{4}}}}

.

Das Apothema eines regelmäßigen n-Ecks der Kantenlänge $l$ ist

a={\frac {l}{2\,\tan {\frac {180^{\circ }}{n}}}}

.

Damit kann sein Flächeninhalt zu $A={\tfrac {1}{2}}\cdot n\cdot l\cdot a$ ermittelt werden. Für verschiedene $n$ ergeben sich die folgenden Werte:

regelmäßiges Vieleck	Seitenlänge	Apothema	Fläche
Dreieck	$l=r\cdot {\sqrt {3}}$	$a=r\cdot {\tfrac {1}{2}}$	$A=r^{2}\cdot {\tfrac {3{\sqrt {3}}}{4}}$
Viereck	$l=r\cdot {\sqrt {2}}$	$a=r\cdot {\tfrac {1}{2}}{\sqrt {2}}$	$A=r^{2}\cdot 2$
Fünfeck	$l=r\cdot {\sqrt {{\tfrac {1}{2}}(5-{\sqrt {5}})}}$	$a=r\cdot {\tfrac {1}{4}}(1+{\sqrt {5}})$	$A=r^{2}\cdot {\tfrac {5}{8}}{\sqrt {(10+2{\sqrt {5}})}}$
Sechseck	$l=r\,$	$a=r\cdot {\tfrac {1}{2}}{\sqrt {3}}$	$A=r^{2}\cdot {\tfrac {3}{2}}{\sqrt {3}}$
Achteck	$l=r\cdot {\sqrt {2-{\sqrt {2}}}}$	$a=r\cdot {\sqrt {{\tfrac {1}{2}}+{\tfrac {1}{4}}{\sqrt {2}}}}$	$A=r^{2}\cdot 2{\sqrt {2}}$
$n$ -Eck	$l=r\cdot 2\cdot \sin {\tfrac {180^{\circ }}{n}}$	$a=r\cdot \cos {\tfrac {180^{\circ }}{n}}$	$A=r^{2}\cdot {\tfrac {n}{2}}\cdot \sin {\tfrac {360^{\circ }}{n}}$
$n\to \infty$ (Kreis)	$l\to 0$	$a\to r$	$A\to r^{2}\cdot \pi$

Siehe auch

Sagitta-Methode

Weblinks

Commons: Chord (geometry) – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Apothema – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Eric W. Weisstein: Apothem. In: MathWorld (englisch).
Sagitta, Apothem, and Chord Ed Pegg, Jr., The Wolfram Demonstrations Project

Einzelnachweise

Paul Huther: Anfangsgründe der Geometrie vorzüglich zum Gebrauche an technischen Schulen. G. Joseph Manz, Regensburg 1838, eingeschränkte Vorschau in der Google-Buchsuche.
J. Michael Köberlein: Lehrbuch der Elementar-Geometrie und Trigonometrie zunächst für Gymnasien und Lyzeen. J. E. von Seidel, Sulzbach 1824, eingeschränkte Vorschau in der Google-Buchsuche.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Paul Huther: Anfangsgründe der Geometrie vorzüglich zum Gebrauche an technischen Schulen. G. Joseph Manz, Regensburg 1838, eingeschränkte Vorschau in der Google-Buchsuche.

[2] J. Michael Köberlein: Lehrbuch der Elementar-Geometrie und Trigonometrie zunächst für Gymnasien und Lyzeen. J. E. von Seidel, Sulzbach 1824, eingeschränkte Vorschau in der Google-Buchsuche.