Anomalie (Quantenfeldtheorie)

Unter einer Anomalie in der Quantenfeldtheorie versteht man die Brechung einer klassischen Symmetrie einer Feldtheorie (auf klassischem Niveau) durch den Prozess der Quantisierung.

Vom Standpunkt der Quantenfeldtheorie betrachtet ist die Bezeichnung Anomalie eigentlich nicht sinnvoll, denn im klassischen Limes $\hbar \to 0$ verschwinden die (zu den Erhaltungssätzen gehörenden) Symmetrien nicht, sondern die Wirkungsterme dominieren alle anderen.

Technische Beschreibung

Technisch gesehen ergeben sich solche anomalen Symmetrien, indem zwar das Wirkungsfunktional ${\mathcal {A}}$ der Feldtheorie, d. h. ihre Lagrangedichte, der Symmetrie gehorcht, aber nicht die bei der Quantisierung benötigten Maßfunktionen $\mu$ und somit auch nicht das Erzeugende Funktional ${\mathcal {Z}}=\int d\mu \,\exp({\mathcal {A}}/\hbar )$ der Theorie; dabei sind $\,\hbar$ das reduzierte plancksche Wirkungsquantum und $\exp$ die Exponentialfunktion.

Relevanz und Anwendungen

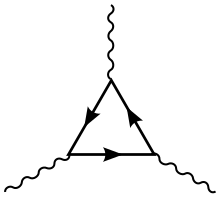
Das Dreiecksdiagramm: Die Wellenlinien stehen für Photonen; die nach rechts bzw. links gerichteten durchgezogenen Linien bezeichnen Elektronen bzw. Positronen.

Die physikalische Relevanz solcher Anomalien drückt sich u. a. dadurch aus, dass sie einen wesentlichen Beitrag zu den Zerfällen des neutralen Pions liefern ( $\pi ^{0}\rightarrow \gamma \gamma$ bzw. $\pi ^{0}\rightarrow e^{+}e^{-}\gamma$ ), und zwar im Zusammenhang mit dem Dreiecksdiagramm. (Dass beim vollständigen Umlauf um das Dreieck ein Positron in ein Elektron umgewandelt wird, ist eine explizite Signatur des anomalen Verhaltens.)

Andere Beispiele ergeben sich bei den Ward-Identitäten. Dabei handelt es sich um Gleichungen für quantenmechanische Amplituden, die in quantisierten Theorien an die Stelle der (durch die Quantisierung ungültig gewordenen) Erhaltungssätze treten.

Außerdem erklären die Anomalien das Fehlen eines neunten Goldstone-Bosons, das ansonsten von der QCD gefordert würde.

Anomaliefreiheit von Eichsymmetrien

Während Anomalien globaler Symmetrien harmlos sind und wie im Beispiel des $\pi ^{0}$ -Zerfalls auch in der Natur beobachtet werden, würden Anomalien bei den Eichsymmetrien, die lokal sind, die Renormierbarkeit der Theorie zerstören. Daher müssen Eichsymmetrien aus Konsistenzgründen immer anomaliefrei sein.

Für die Eichsymmetrie des Standardmodells ist dies dadurch gewährleistet, dass sich die anomalen Beiträge der verschiedenen Flavors von Quarks und Leptonen gerade gegenseitig aufheben, solange die Zahl der Generationen im Quark- und Leptonsektor gleich ist.

Literatur

Barry R. Holstein: Anomalies for pedestrians. In: Am. J. Phys. Band 61, Nr. 2, 1993, S. 142–147, doi:10.1119/1.17328.
Reinhold A. Bertlmann: Anomalies in quantum field theory. Oxford University Press, Oxford 2000, ISBN 0-19-850762-3.
Roman W. Jackiw: Axial anomaly. In: Scholarpedia. Band 3, Nr. 10, 2008, S. 7302, doi:10.4249/scholarpedia.7302.

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.