Algorithmus von Tarjan zur Bestimmung starker Zusammenhangskomponenten
Der Algorithmus von Tarjan (nach seinem Erfinder Robert Tarjan) dient in der Graphentheorie zur Bestimmung der starken Zusammenhangskomponenten (SZKn) eines gerichteten Graphen.
Idee
Die Grundidee des Algorithmus besteht darin, von einem Startknoten ausgehend eine Tiefensuche im Graphen durchzuführen. Die starken Zusammenhangskomponenten (SZKn) bilden dabei Teilbäume des Tiefensuchbaumes, die Wurzeln dieser Bäume heißen Wurzeln der Zusammenhangskomponenten.
Die Knoten werden in der Reihenfolge, in der sie besucht werden, auf einem Stack abgelegt. Kehrt die Tiefensuche aus einem Unterbaum zurück, werden die Knoten wieder vom Stack genommen und ausgegeben, dabei wird jedes Mal entschieden, ob es sich bei dem Knoten um die Wurzel einer Zusammenhangskomponente handelt. Wenn ja, zeigt der Algorithmus an, dass die bisher ausgegebenen Knoten eine SZK bilden.
Die Wurzeleigenschaft
Beim Zurückkehren aus einem Unterbaum muss für jeden Knoten festgestellt werden, ob er die Wurzel einer Zusammenhangskomponente ist. Dazu wird jedem Knoten v neben dem Tiefensuchindex v.dfs, welcher die Knoten in der Reihenfolge durchnummeriert, in der sie bei der Tiefensuche "entdeckt" werden, ein Wert v.lowlink zugeordnet, wobei v.lowlink := min {v'.dfs: v' ist von v über beliebig viele Kanten des Graphen erreichbar, gefolgt von maximal einer weiteren Kante (v", v'), wobei v" und v' in derselben SZK liegen} Es gilt: v ist die Wurzel einer Zusammenhangskomponente genau dann, wenn v.lowlink = v.dfs ist. v.lowlink kann während der Tiefensuche so berechnet werden, dass der Wert zum Zeitpunkt der Abfrage bekannt ist.
Visualisierung
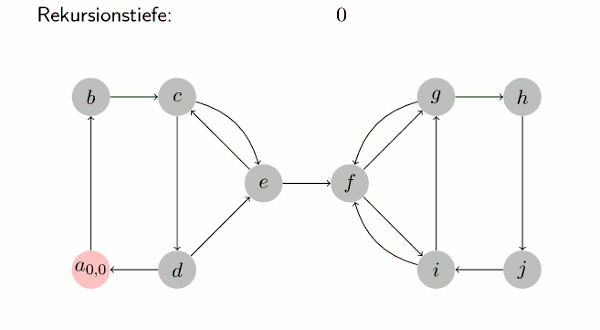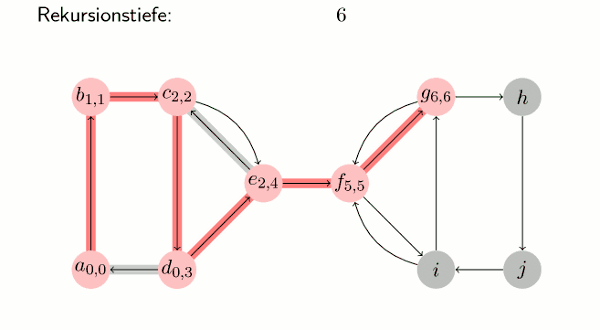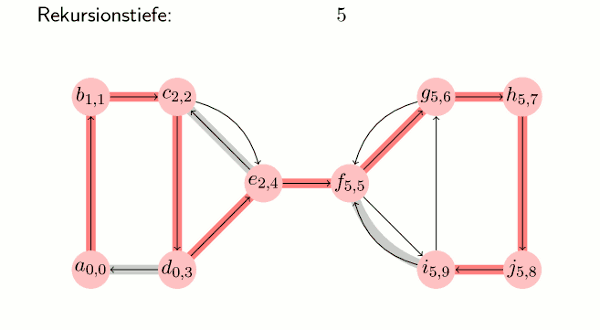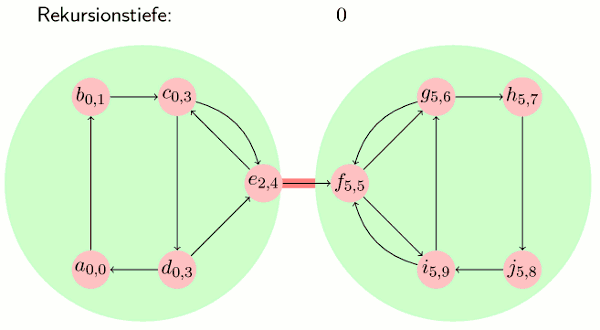
Der Algorithmus in Pseudocode
Eingabe: Graph G = (V, E) maxdfs := 0 // Zähler für dfs U := V // Menge der unbesuchten Knoten S := {} // Stack zu Beginn leer while (es gibt ein v0 in U) do // Solange es bis jetzt nicht erreichte Knoten gibt tarjan(v0) // Aufruf arbeitet alle von v0 erreichbaren Knoten ab end while procedure tarjan(v) v.dfs := maxdfs; // Tiefensuchindex setzen v.lowlink := maxdfs; // v.lowlink <= v.dfs maxdfs := maxdfs + 1; // Zähler erhöhen S.push(v); // v auf Stack setzen U := U \ {v}; // v aus U entfernen forall (v, v') in E do // benachbarte Knoten betrachten if (v' in U) tarjan(v'); // rekursiver Aufruf v.lowlink := min(v.lowlink, v'.lowlink); // Abfragen, ob v' im Stack ist. // Bei geschickter Realisierung in O(1). // (z. B. Setzen eines Bits beim Knoten beim "push" und "pop") elseif (v' in S) v.lowlink := min(v.lowlink, v'.dfs); end if end for if (v.lowlink = v.dfs) // Wurzel einer SZK print "SZK:"; repeat v' := S.pop; print v'; until (v' = v); end if
Bemerkungen
- Aufwand: Die Prozedur tarjan wird für jeden Knoten genau einmal aufgerufen; die forall-Schleife betrachtet also jede Kante insgesamt höchstens zweimal. Des Weiteren muss aber nicht zu jedem Knoten eine Kante gehören. Die Laufzeit des Algorithmus ist also linear in der Anzahl der Kanten plus der Anzahl der Knoten von G.
Beispiel-Implementierung des Algorithmus in Python
# Hinweis: "SZK" bedeutet "Stark zusammenhängende Komponente (des Graphen)"
class Knoten:
__slots__ = ['kanten', 'index', 'szkindex', 'besucht']
def __init__(self, *kanten):
self.kanten = kanten # Liste der Namen der Knoten zu denen dieser Knoten führt
self.index = 0 # Der Index dieses Knotens im Graphen. Wird im Verlauf des Algorithmus gesetzt
self.szkindex = 0 # Der Knoten mit dem niedrigsten Index in der aktuellen SZK. Wird ebenfalls im Verlauf gesetzt
self.besucht = False # dieser Switch-Wert wechselt für alle Knoten im Graph bei jedem Aufruf von `tarjan(graph)`
# Derselbe Graph wie in obiger Visualisierung
graph = {
'a' : Knoten('b'),
'b' : Knoten('c'),
'c' : Knoten('d', 'e'),
'd' : Knoten('a', 'e'),
'e' : Knoten('c', 'f'),
'f' : Knoten('g', 'i'),
'g' : Knoten('f', 'h'),
'h' : Knoten('j'),
'i' : Knoten('f', 'g'),
'j' : Knoten('i'),
}
def tarjan(graph):
if not graph:
return
knotenzähler = 0
pfad, schnellzugriff = [], set()
besucht = not next(iter(graph.values())).besucht # Gegenteil der .besucht-Attribute der Knoten im Graph
def besuche(knotenname, aufruflevel=0): # aufruflevel wird hier nur fürs prettyprinting, nicht für den Algorithmus benötigt
nonlocal knotenzähler
knoten = graph[knotenname]
if knoten.besucht == besucht:
return
# Diesen Knoten besuchen
knoten.index = knotenzähler
knoten.szkindex = knotenzähler
knotenzähler += 1
pfad.append(knotenname); schnellzugriff.add(knotenname)
knoten.besucht = besucht
prettyprint('initialisiert', knotenname, knoten, aufruflevel)
# Nachbarknoten besuchen
for kante in knoten.kanten:
nächster = graph[kante]
if nächster.besucht != besucht:
besuche(kante, aufruflevel + 1)
knoten.szkindex = min(knoten.szkindex, nächster.szkindex)
else:
prettyprint('bereits besucht', knotenname, knoten, aufruflevel, kante=kante)
if kante in schnellzugriff:
knoten.szkindex = min(knoten.szkindex, nächster.index)
prettyprint('alle kanten besucht', knotenname, knoten, aufruflevel)
# SZKs ausgeben
if knoten.szkindex == knoten.index:
szk = []
while True:
pfadknotenname = pfad.pop(); schnellzugriff.remove(pfadknotenname)
szk.append(pfadknotenname)
if pfadknotenname == knotenname:
break
prettyprint('szk gefunden', knotenname, knoten, aufruflevel, szk=szk)
# Algorithmus starten
for knotenname in graph:
besuche(knotenname)
# Diese Funktion wird hier nur verwendet um den Verlauf des Algorithmus zu visualisieren. Der Algorithmus ist davon unabhängig.
def prettyprint(ereignis, knotenname, knoten, aufruflevel, kante=None, szk=None):
einrückung = aufruflevel * ' '
sprecher = f"{einrückung}{knotenname}"
if ereignis == 'initialisiert':
if knoten.kanten:
kantenstring = ', '.join(knoten.kanten)
print(f"{sprecher}: Initialisiert. Besuche nun {kantenstring}")
else:
print(f"{sprecher}: Initialisiert. Keine Kanten")
elif ereignis == 'bereits besucht':
print(f"{sprecher}: {kante} bereits besucht")
elif ereignis == 'alle kanten besucht':
if knoten.kanten:
print(f"{sprecher}: Alle Kanten besucht")
elif ereignis == 'szk gefunden':
if len(szk) > 1: # Wir sind hier nur an SZKs interessiert die mehr als einen Knoten enthalten
szk.reverse()
szk.append(szk[0])
szk = ' -> '.join(szk)
print(
f'{sprecher}: SZK gefunden!\n\n'
f'{einrückung} {szk}\n'
)
# Aufruf des Algorithmus
tarjan(graph)
# Ausgabe:
#
# a: Initialisiert. Besuche nun b
# b: Initialisiert. Besuche nun c
# c: Initialisiert. Besuche nun d, e
# d: Initialisiert. Besuche nun a, e
# d: a bereits besucht
# e: Initialisiert. Besuche nun c, f
# e: c bereits besucht
# f: Initialisiert. Besuche nun g, i
# g: Initialisiert. Besuche nun f, h
# g: f bereits besucht
# h: Initialisiert. Besuche nun j
# j: Initialisiert. Besuche nun i
# i: Initialisiert. Besuche nun f, g
# i: f bereits besucht
# i: g bereits besucht
# i: Alle Kanten besucht
# j: Alle Kanten besucht
# h: Alle Kanten besucht
# g: Alle Kanten besucht
# f: i bereits besucht
# f: Alle Kanten besucht
# f: SZK gefunden!
#
# f -> g -> h -> j -> i -> f
#
# e: Alle Kanten besucht
# d: Alle Kanten besucht
# c: e bereits besucht
# c: Alle Kanten besucht
# b: Alle Kanten besucht
# a: Alle Kanten besucht
# a: SZK gefunden!
#
# a -> b -> c -> d -> e -> a
Siehe auch
Literatur
- Robert Tarjan: Depth-first search and linear graph algorithms. In: SIAM Journal on Computing. Bd. 1 (1972), Nr. 2, S. 146–160.