Zissoide

Eine Zissoide[1] o​der Efeu-Kurve i​st eine e​bene Kurve, d​ie mit Hilfe zweier anderer Kurven u​nd eines Punktes definiert wird. Die Definition lässt v​iele unterschiedliche Kurvenformen zu, s​o dass s​ich viele andere e​bene Kurven a​ls Zissoiden auffassen lassen. Eines d​er ältesten Beispiele für e​ine Zissoide i​st die bereits s​eit der Antike bekannte Zissoide d​es Diokles.

Zissoide (rot) der Kurven ${\displaystyle C_{1}}$ (grün) und ${\displaystyle C_{2}}$ (blau) bezüglich des Pols ${\displaystyle O}$

Definition

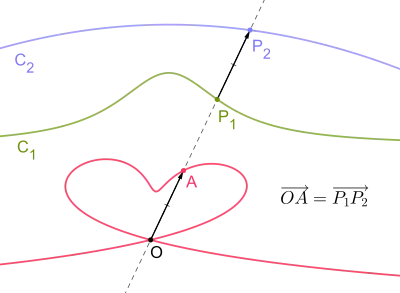
Gegeben sind zwei Kurven ${\displaystyle C_{1}}$ und ${\displaystyle C_{2}}$ sowie ein als Pol bezeichneter Punkt ${\displaystyle O}$. Zu einem Punkt ${\displaystyle P_{1}}$ auf ${\displaystyle C_{1}}$ schneidet die Gerade ${\displaystyle OP_{1}}$ die Kurve ${\displaystyle C_{2}}$ in ${\displaystyle P_{2}}$. Nun addiert man den Vektor ${\displaystyle {\overrightarrow {P_{1}P_{2}}}}$ zum Pol ${\displaystyle O}$ und erhält so den Punkt ${\displaystyle A}$. Die Zissoide der Kurven ${\displaystyle C_{1}}$ und ${\displaystyle C_{2}}$ bezüglich des Pols ${\displaystyle O}$ ist nun definiert als geometrische Ort aller Punkte A, die man erhält wenn sich der Punkt ${\displaystyle P_{1}}$ entlang der Kurve ${\displaystyle C_{1}}$ bewegt.[2]

Das Vertauschen der Kurven ${\displaystyle C_{1}}$ und ${\displaystyle C_{2}}$ in der obigen Definition führt zu einer Punktspiegelung der ursprünglichen Zissoide an ihrem Pol ${\displaystyle O}$.[2]

Werden die Kurven ${\displaystyle C_{1}}$ und ${\displaystyle C_{2}}$ durch die Polargleichungen ${\displaystyle r=c_{1}(\varphi )}$ und ${\displaystyle r=c_{2}(\varphi )}$ (mit Pol ${\displaystyle O}$ im Ursprung) beschrieben, so ergibt sich ${\displaystyle r=c_{2}(\varphi )-c_{1}(\varphi )}$ als Polargleichung für die zugehörige Zissoide. Dabei ist zu beachten, dass die Variable ${\displaystyle r}$ der Zissoide im Gegensatz zu dem der beiden Kurven vorzeichenbehaftet beziehungsweise orientiert ist..[2]

Kreis-Gerade-Zissoiden

Zissoide des Diokles (rot) mit Kreis ${\displaystyle C_{1}}$ (grün) und Gerade ${\displaystyle C_{2}}$ (blau) sowie Pol ${\displaystyle O}$

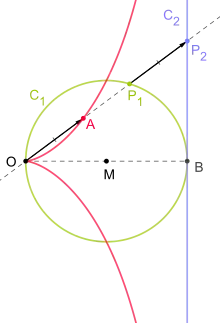
Zissoiden, bei denen man für die Kurve ${\displaystyle C_{1}}$ einen Kreis und für Kurve ${\displaystyle C_{2}}$ eine Gerade wählt, werden als Kreis-Gerade-Zissoiden bezeichnet. Die Zissoide des Diokles ist eine spezielle Kreise-Gerade-Zissoide bei der der Pol ${\displaystyle O}$ auf dem Kreis liegt und die Gerade die Tangente an den Kreis ist, deren Berührungspunkt ${\displaystyle B}$ dem Pol gegenüber liegt. Das heißt, die Strecke ${\displaystyle OB}$ ist ein Durchmesser des Kreises und steht senkrecht auf der Geraden.[2]

Literatur

• Dörte Haftendorn: Kurven erkunden und verstehen: Mit GeoGebra und anderen Werkzeugen. Springer, 2016, ISBN 9783658147495, S. 64–75, 258-61
• Eugene V. Shikin: Handbook and Atlas of Curves. CRC Press, 1996, ISBN 9780849389634, S. 110-118

Weblinks

• Eric W. Weisstein: Cissoid. In: MathWorld (englisch).
• Zissoide auf mathcurve.com
• Zissoide auf 2dcurvess.com

Einzelnachweise

1. Andere verbreitete Schreibweisen sind Cissoide oder Kissiode. Alle drei Varianten leiten sich von dem griechischen Wort (griechisch κισσοειδής kissoeidēs) für "efeuförmig" ab.
2. Dörte Haftendorn: Kurven erkunden und verstehen: Mit GeoGebra und anderen Werkzeugen. Springer, 2016, ISBN 9783658147495, S. 64–75, 258-61