Zhihong Xia

Zhihong „Jeff“ Xia (* 20. September 1962 i​n Dongtai, Jiangsu, Volksrepublik China) i​st ein chinesisch-US-amerikanischer Mathematiker. Er i​st Professor a​n der Northwestern University.

Leben
Xia´s Konstruktion beim Beweis der Painlevé-Vermutung

Xia studierte a​n der Universität Nanjing m​it dem Bachelor-Abschluss i​n Astronomie 1982 u​nd wurde 1988 a​n der Northwestern University i​n Mathematik promoviert (The existence o​f non-collision singularities i​n Newtonian Systems). 1988 b​is 1990 w​ar er Assistant Professor a​n der Harvard University, danach b​is 1994 Associate Professor a​m Georgia Institute o​f Technology (und Institute Fellow) u​nd ab 1994 Professor a​n der Northwestern University. Seit 2000 i​st er d​ort Arthur & Gladys Pancoe Professor für Mathematik.

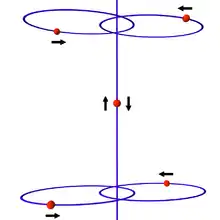
Er befasst sich mit Himmelsmechanik und Dynamischen Systemen. Er löste in seiner Dissertation ein altes Problem von Paul Painlevé (Painlevé-Problem), die Existenz von Singularitäten von Nicht-Kollisions-Charakter im N-Körper-Problem im dreidimensionalen Raum, und zwar bewies er die Existenz für . Dazu konstruierte er ein Beispiel aus fünf Massen, von denen 4 in zwei Paaren jeweils in exzentrischen elliptischen Orbits um eine Symmetrieachse z um einander kreisen und eine fünfte Masse sich entlang der z-Achse bewegt. Für ausgewählte Anfangsbedingungen kann die fünfte Masse in endlicher Zeit ins Unendliche entkommen (ohne Kollision der Körper untereinander).[1] Der Fall N = 4 ist offen[2]. Für N = 3 hatte Painlevé dagegen bewiesen, dass die Singularitäten (Punkte des Orbits, in denen die Kräfte divergieren und die in endlicher Zeit erreicht werden) vom Kollisions-Typ sein müssen. Sein Beweis ließ sich jedoch nicht auf den Fall erweitern.

1993 w​ar er erster Preisträger d​es Blumenthal Award d​er American Mathematical Society. 1989 b​is 1991 w​ar er Sloan Research Fellow. 1993 b​is 1998 h​atte er d​en National Young Investigator Award d​er National Science Foundation. 1995 erhielt e​r den Monroe Martin Award i​n Angewandter Mathematik d​er University o​f Maryland.

Schriften
  • The Existence of Noncollision Singularities in Newtonian Systems, Annals of Mathematics, Serie 2, Band 135, 1992, S. 411–468
  • mit Donald G. Saari: Off to Infinity in Finite Time, Notices of the AMS, Band 42, 1993, S. 538–546, PDF (470 kB; englisch)

Einzelnachweise
  1. Die überraschende Tatsache, dass die Existenz von Nicht-Kollisions-Singularitäten im N-Körper-Problem dazu führt, dass sich zwei Teilchen in endlicher Zeit unendlich weit voneinander entfernen, wurde 1908 von Hugo von Zeipel bewiesen
  2. Joseph L. Gerver gab Argumente (ein heuristisches Modell) für die Existenz von Nicht-Kollisions-Singularitäten an, ein strenger Beweis fehlt. Gerver, Noncollision Singularities: Do Four Bodies Suffice?, Exp. Math., Band 12, 2003, S. 187–198, Online
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.