Zentrierte Polygonalzahl
Eine zentrierte Polygonalzahl ist eine Zahl, zu der sich ein regelmäßiges Polygon (Vieleck) in einem bestimmten Muster und mit einer entsprechenden Zahl an Steinen legen lässt. Das Legemuster beginnt mit einem einzelnen Stein im Mittelpunkt des Polygons. Um diesen Zentrumsstein werden weitere Polygone gelegt, wobei sich deren Seitenlängen von innen nach außen jeweils um eins erhöhen. Abhängig von der Anzahl der Seiten spricht man beispielsweise von zentrierten Dreieckszahlen, zentrierten Quadratzahlen, zentrierten Fünfeckszahlen, zentrierten Sechseckszahlen, und so weiter. Aufgrund ihrer Verwandtschaft mit einer geometrischen Figur zählen die zentrierten Polygonalzahlen zur Klasse der figurierten Zahlen. Eine andere Art, Zahlen auf Polygone zurückzuführen, stellen die (dezentralen) Polygonalzahlen dar.
Beispiele
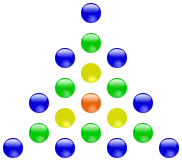 Die 19 ist die vierte zentrierte Dreieckszahl.
Die 19 ist die vierte zentrierte Dreieckszahl.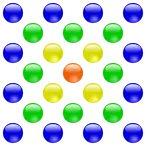 Die 25 ist die vierte zentrierte Quadratzahl.
Die 25 ist die vierte zentrierte Quadratzahl.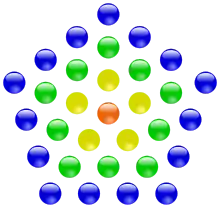 Die 31 ist die vierte zentrierte Fünfeckszahl.
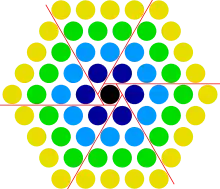
Die 31 ist die vierte zentrierte Fünfeckszahl.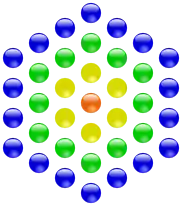 Die 37 ist die vierte zentrierte Sechseckszahl.
Die 37 ist die vierte zentrierte Sechseckszahl.
Berechnung
Die -te zentrierte -Eckszahl berechnet sich nach der Formel
- .
Alternativ kann man die -te zentrierte -Eckszahl auch mit Hilfe der -ten Dreieckszahl nach der Formel
berechnen.
Neben einer anschaulichen Erklärung lässt sich die Formel auch algebraisch beweisen. Nach dem angegebenen Bildungsprinzip, dem Zeichnen von -Ecken mit um eins steigender Seitenlänge um einen Anfangspunkt, lässt sich die -te -Eckzahl durch
ausdrücken.
- .
Literatur
- Lancelot Hogben: Mathematik für alle. Eine Einführung in die Wissenschaft der Zahlen und Figuren. Neu überarbeitete Ausgabe. Pawlak, Herrsching 1985, ISBN 3-88199-208-1, S. 151ff.