Zählprozess

Ein Zählprozess ist ein spezieller stochastischer Prozess. Er zählt die Anzahl der Ereignisse eines bestimmten Typs, die bis zu einem Zeitpunkt eingetreten sind.

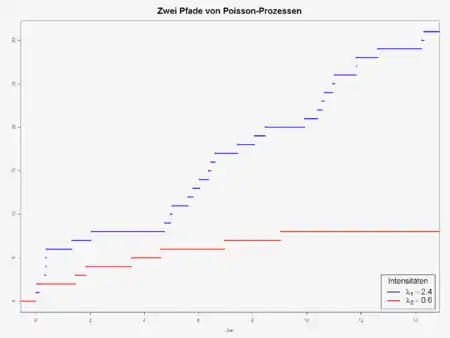
Beispiel eines Zählprozesses: der Poisson-Prozess, hier mit verschiedenen Intensitäten

Anwendung und Beispiele

Zählprozesse spielen bei der Modellierung und Simulation von Bedienungssystemen eine Rolle, praktikabel ist die Simulation meist jedoch nur für spezielle Zählprozesse, insbesondere Erneuerungsprozesse durch ereignisorientierte Simulation.

Als ein Beispiel eines Zählprozesses kann der Poisson-Prozess genannt werden, der auch ein Erneuerungsprozess ist. Einige Theorien lassen sich mittels Zählprozessen darstellen. Beispielsweise lässt sich die gesamte Überlebenszeitanalyse mittels der Zählprozesstheorie darstellen.

Definition

Ein stochastischer Prozess $N=(N(t))_{t\geq 0}$ heißt Zählprozess[1], wenn es eine Folge positiver Zufallsgrößen $(Y_{n})_{n\in \mathbb {N} }$ , die sogenannten Zwischenankunftszeiten, derart gibt, dass mit $S_{n}:=Y_{1}+\dotsb +Y_{n}$ gilt:

$N(t)=\left\{{\begin{matrix}0,&{\mbox{falls }}t<Y_{1}\\\max \left\{n\in \mathbb {N} :S_{n}\leq t\right\},&{\mbox{sonst}}\end{matrix}}\right.$

Die Folge der $S_{n}$ bildet dann einen Punktprozess auf $\mathbb {R} ^{+}$ . Dieser positioniert zufällige Punkte auf der positiven Zahlengerade, deren Abstände gemäß den Zwischenankunftszeiten verteilt sind. Der Zählprozess läuft dann mit konstanter Geschwindigkeit die positiven Zahlen ab und zählt, wie viele Punkte er bis zum Zeitpunkt $t$ bereits angetroffen hat. Aufgrund dieser engen Verbindung werden Zählprozess und Punktprozess teils auch synonym verwendet.[2]

Die Pfade eines Zählprozesses sind also Sprungfunktionen mit Sprunghöhe 1.

Einzelnachweise

Jochen Wengenroth: Wahrscheinlichkeitstheorie. de Gruyter, Berlin 2008, ISBN 978-3-11-020358-5, S. 127 (eingeschränkte Vorschau in der Google-Buchsuche).
Eric W. Weisstein: PointProcess. In: MathWorld (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Jochen Wengenroth: Wahrscheinlichkeitstheorie. de Gruyter, Berlin 2008, ISBN 978-3-11-020358-5, S. 127 (eingeschränkte Vorschau in der Google-Buchsuche).

[2] Eric W. Weisstein: PointProcess. In: MathWorld (englisch).