Wurzelortskurve

Die Wurzelortskurve (WOK) ist eine grafische Darstellung der Lage der Polstellen und Nullstellen der komplexen Führungs-Übertragungsfunktion F₀(s) eines Regelkreises in Abhängigkeit von einem Parameter und wird im Bereich der Regelungstechnik zu Stabilitätsuntersuchungen eingesetzt. Das Verfahren der Wurzelortskurve kann sowohl in der komplexen s-Ebene, für kontinuierliche Systeme, als auch in der komplexen z-Ebene für zeitdiskrete Systeme angewendet werden. Das Verfahren wurde 1948 vom US-amerikanischen Regelungstechniker Walter Richard Evans entwickelt.[1]

Allgemeines

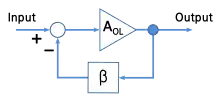
System A_ol (Regelstrecke) mit Rückkopplung über ein P-Glied mit dem Faktor β

Die Stabilität eines Systems wird durch die Position seiner Polstellen in der komplexen Ebene bestimmt. Beispielsweise und anhand der nebenstehenden Abbildung dargestellt, bewirken bei dem zeitkontinuierlichen System A_ol Polstellen in der Übertragungsfunktion in der rechten s-Halbebene, d. h. mit positiven Realteil, eine Instabilität. Durch die Möglichkeit einer Rückkopplung lässt sich die Position dieser Polstellen in der komplexen Ebene bei dem rückgekoppelten System verschieben, die Wurzelortskurve stellt dabei grafisch eine Möglichkeit dar, diese Polstellenverschiebung zu veranschaulichen.

In der rechten Abbildung ist die Rückkopplung im einfachsten Fall mit einem konstanten Faktor β dargestellt. Die Systemfunktion ist beispielhaft und der Einfachheit wegen als ein System 1. Ordnung gegeben:

A_{OL}={\frac {b}{s-a}}

Für $a>0,b>0$ ist dieses System instabil, da die Polstelle rechts der imaginären Achse liegt. Die Übertragungsfunktion des rückgekoppelten Systems zwischen Eingang und Ausgang ist:

G(s)={\frac {A_{OL}}{1+\beta A_{OL}}}={\frac {b}{s-a+\beta \cdot b}}

und besitzt eine Polstelle bei $s=a-\beta \cdot b$ . In der Wurzelortskurve wird die Verschiebung der Polstelle als Funktion des Verstärkungsfaktors β grafisch dargestellt. In diesem Fall wird das rückgekoppelte System für Verstärkungswerte $\beta \geq {\frac {a}{b}}$ stabil. Umgekehrt lässt sich ein stabiles System A_ol mit obiger Systemfunktion und den Parametern $a<0,b>0$ mit einer positiven Rückkopplung $\beta <0$ in ein instabiles rückgekoppeltes System überführen.

Die Wurzelortskurve verdeutlicht die Verschiebung der Polstellen in Abhängigkeit von den Parametern der Rückkopplungen bzw. des Reglers und ermöglicht dadurch Rückschlüsse auf das Stabilitätsverhalten und die Dynamik des Regelkreises. Bei Systemen höher Ordnung nimmt die Verschiebung der Polstellen in der komplexen Ebene kompliziertere Formen an und erfordert im nachfolgenden dargestellte Konstruktionsvorgaben zur Bestimmung.

Definition

Sei im Folgenden G₀ die Übertragungsfunktion des offenen (nicht rückgekoppelten) Systems. Zur Wurzelortskurve gehören alle Punkte der komplexen Ebene, welche die charakteristische Gleichung:

1+k\cdot G_{0}(s)=0

erfüllen. Gilt $\quad 0\leq k<\infty$ , so handelt es sich um die eigentliche Wurzelortskurve, ansonsten um die komplementäre (oder uneigentliche) Wurzelortskurve. Eine Lösung der Gleichung für festes k heißt Wurzelort.

Eigenschaften

Die Wurzelortskurve ist symmetrisch zur reellen Achse. Sie beginnt für $k=0$ in den Polen $s_{i}$ des offenen, korrigierten Kreises (L(s)=H(s)*G(s)) und endet für $k\to \pm \infty$ in seinen Nullstellen $s_{0i}$ . Lösungen für $k\geq 0$ gehören der eigentlichen (positiven) WOK an, die Kurven für $k<0$ gehören zur komplementären (negativen) WOK.

Exakte Konstruktion

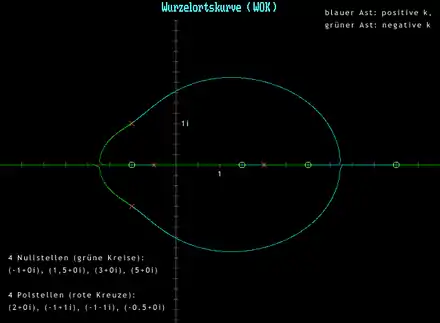
Beispiel einer Wurzelortskurve mit vier Polen und vier Nullstellen

Für die exakte Konstruktion der Wurzelortskurve wird die Übertragungsfunktion der offenen Kette wie folgt zerlegt:

G_{0}(s)=k{\hat {G}}_{0}(s)=k{\frac {\Pi _{i=1}^{q}(s-s_{0i})}{\Pi _{i=1}^{n}(s-s_{i})}}

Darin bezeichnen $n$ die Systemordnung und $q$ die Anzahl der Nullstellen des Systems. Zur Wurzelortskurve gehören alle komplexen Punkte, welche die Amplitudenbedingung und die Phasenbedingung erfüllen:

Amplitudenbedingung:

{\frac {|\Pi _{i=1}^{q}(s-s_{0i})|}{|\Pi _{i=1}^{n}(s-s_{i})|}}={\frac {1}{|k|}}

,

Phasenbedingung:

\sum _{i=1}^{q}\Phi _{0i}-\sum _{i=1}^{n}\Phi _{i}=(2l+1)\pi ,\quad l=0,1,2,...

,

wobei $\Phi _{0i}$ und $\Phi _{i}$ für jede Nullstelle bzw. jeden Pol die mathematisch positiv gezählten Winkel zwischen einem von Nullstelle bzw. Pol gedachten waagerechten nach rechts zeigenden Strahl und dem zu überprüfenden Punkt bezeichnen.

Die Amplitudenbedingung kann auch verwendet werden, um für einen gegebenen Punkt der Wurzelortskurve die zugehörige Verstärkung $k$ zu bestimmen.

Regeln zum Skizzieren

Die Amplituden- und Phasenbedingung kann zur numerischen Konstruktion der Wurzelortskurve durch einen Rechner genutzt werden. Ihre Verwendung zur manuellen Skizzierung ist unhandlich, daher wurden folgende Konstruktionsregeln abgeleitet.

Ursprung/Ende: Jeder Ast der Wurzelortskurve beginnt in einem Pol der offenen Kette $G_{0}$ und endet in einer Nullstelle der offenen Kette, oder im Unendlichen.
Asymptoten: Für große Verstärkungen nähern sich die Äste Geraden asymptotisch an. Die Anzahl der Asymptoten ist $n-q$ . Die Asymptoten haben für $k>0$ Neigungswinkel $\phi _{\mathrm {As} }={\frac {\pi +l\cdot 2\pi }{n-q}},\quad l=0,1,...,n-q-1$ und schneiden sich im gemeinsamen Schnittpunkt (Wurzelschwerpunkt) $s_{\mathrm {As} }={\frac {\sum _{i=1}^{n}s_{i}-\sum _{i=1}^{q}s_{0i}}{n-q}}$ .
Reelle Achse: Zur eigentlichen Wurzelortskurve gehören genau die Punkte $s$ der reellen Achse, für die die Anzahl der von dort aus gesehen rechts gelegenen reellen kritischen Stellen (Nullstellen und Pole) ungerade ist. Alle übrigen Punkte auf der reellen Achse gehören zur komplementären WOK ( $k<0$ ). Jeder Punkt auf der reellen Achse ist also Teil einer WOK: entweder Teil der eigentlichen WOK ( $k>0$ ) oder Teil der komplementären WOK ( $k<0$ ).
Verzweigungs- und Vereinigungspunkte: Verzweigungs- und Vereinigungspunkte sind genau solche Punkte, die sowohl die Phasenbedingung als auch die Gleichung $\sum _{i=1}^{q}{\frac {1}{s-s_{0i}}}=\sum _{i=1}^{n}{\frac {1}{s-s_{i}}}$ erfüllen.

Anwendung

Die Wurzelortskurve ermöglicht die Analyse der Stabilität, wenn der geschlossene Regelkreis $\left(G(s)={\frac {G_{0}(s)}{1+G_{0}(s)}}\right)$ gegeben ist, ohne die Führungs-Übertragungsfunktion $G(s)$ explizit auszurechnen. Wenn alle Pole und Nullstellen in $Re(-)$ (offene linke Halbebene) liegen, ist der geschlossene Regelkreis stabil. Befinden sich ein oder mehrere Pole in $Re(+)$ (offene rechte Halbebene), ist das System instabil. Befinden sich ein oder mehrere Pole auf der imaginären Achse und alle restlichen Pole in der linken Halbebene, so spricht man von einem bedingt stabilen oder grenzstabilen System. Befinden sich alle Pole auf der imaginären Achse (Realteil gleich 0), so handelt es sich um ein ungedämpftes System. Existiert ein komplex-konjungiertes Polpaar so ist das System schwingungsfähig. Befindet sich dieses in der linken Halbebene, so ist das System gedämpft schwingungsfähig (abklingende Schwingung). Befindet sich das komplex konjugierte Polpaar in der rechten Halbebene, so führt das System eine aufklingende (angefachte) Schwingung aus, und ist damit instabil.

Die Wurzelortskurve ist für lineare und zeitinvariante Systeme wie beispielsweise PID-Regler geeignet. Als freier Parameter wird meist die Verstärkung genommen, was für einen Reglerentwurf durch das Wurzelortskurvenverfahren ausgenutzt wird.

Amplitudenrand, linksseitiger Abstand, Dämpfungsgrad, Wurzelwinkel

Für den Systementwurf ist die absolute Aussage über die Stabilität eine Grundvoraussetzung, jedoch oft nicht hinreichend. Es wird grundsätzlich auch eine Aussage über die Güte der Stabilität gefordert. Konkret sind Maßzahlen zu ermitteln, die aussagen, ob das System sich wunschgemäß verhält – beispielsweise seine Entfernung von der Stabilitätsgrenze oder sein Beruhigungsverhalten.

Die Stabilitätsgrenze der Wurzelorte ist die imaginäre Achse. Überschreitet die dominante Wurzel die imaginäre Achse, so kann jedem ihrer Orte ein Abstand zu diesem Grenzübergang zugeordnet werden. Dieser Abstand ist primär im Wertebereich des Parameters zu suchen.

Ein relatives Abstandsmaß ist der Amplitudenrand $A_{R}$ . Er bezieht den Wert des Parameters $k$ auf seinen Wert für Grenzstabilität $k_{\text{kritisch}}$ und besagt, mit welchem Faktor der Parameter $k$ vergrößert oder verkleinert werden muss, damit Grenzstabilität eintritt.

A_{R}={\frac {k}{k_{\text{kritisch}}}}

Für $k_{\text{kritisch}}=0$ tritt der Parameter $k$ als absolutes Abstandsmaß auf.

Überschreitet die Wurzelortskurve die imaginäre Achse nicht, kann kein Amplitudenrand bestimmt werden.

Für solche Systeme kann aber möglicherweise der linksseitige Abstand der dominanten Wurzel zur imaginären Achse als Gütemaß betrachtet werden. Allerdings fehlt hier ein klar definierter Bezugspunkt. Man kann beispielsweise den linksseitigen Abstand der dominanten Wurzel ins Verhältnis setzen mit ihrem Abstand für $k=0$ ; man erhält so etwas wie einen Stabilisierungsfaktor $S$ .

S={\frac {\sigma }{\sigma _{0}}}={\frac {re\{s\}}{re\{s_{k=0}\}}}

Ist der Parameter $k$ die Schleifenverstärkung eines einschleifigen Systems, so ist $S$ das Verhältnis zwischen den Abklinkonstanten der geschlossenen Schleife und der offenen Schleife.

Für komplexe dominante Wurzeln wird auch oft ihr Dämpfungsgrad $D$ als Stabilitätsmaß genannt, entsprechend dem Winkel $2\alpha$ , welchen die dominanten Wurzel einschließen. Hierbei nimmt man Bezug auf das Verhalten des PT₂-Systems mit der charakteristischen Gleichung

0=s^{2}+2D\omega _{0}s+\omega _{0}^{2}

Gemäß den Lösungen $s$ dieser Gleichung ergeben sich für Dämpfungsgrad $D$ und Winkel $\alpha$ konjugiert komplexer Wurzeln:

\tan {\alpha }=\left\vert {\frac {im\{s\}}{re\{s\}}}\right\vert

sowie

\cos {\alpha }=D={\frac {\left\vert re\{s\}\right\vert }{\left\vert s\right\vert }}

.

Der über den Winkel definierte Dämpfungsgrad $D$ des dominanten Wurzelpaares gibt Auskunft über die Qualität der Sprungantwort; er bestimmt maßgeblich die Stärke des Überschwingens und damit das Beruhigungsverhalten. Beim System 2. Ordnung ist der Dämpfungsgrad $D$ proportional dem linksseitigen Abstand der komplexen Wurzeln von der imaginären Achse, wodurch $D$ auch ein direktes Stabilitätsmaß für dieses System darstellt. Als Bezugspunkte wurden festgelegt:

der Grenzstabile Fall mit $D=0$ (hier ist $\alpha$ = 90°),
der Aperiodische Grenzfall mit $D=1$ (hier ist $\alpha$ = 0°),

wobei der Aperiodische Grenzfall auch gleichzeitig den größtmöglichen Abstand der Wurzeln zur imaginären Achse vertritt. Für Systeme höherer Ordnung können (müssen aber nicht) die Verhältnisse anders liegen. Ein kleinerer Winkel $\alpha$ bedeutet hier nicht automatisch ein höheres Stabilitätsmaß. Öffnungsrichtung und Lage der komplexen Figur können gänzlich verschieden sein vom System 2. Ordnung.

Für die Charakterisierung der Stabilität eines unbekannten Systems kann deshalb das Dämpfungsmaß allein ungeeignet sein. Aus diesem Grund wird als Stabilitätsmaß meist nur der Abstand $re{s}$ zur imaginären Achse herangezogen und der maximale Öffnungswinkel der Wurzelortskurve als weiteres Kriterium gefordert.

Für Systeme, von denen man bereits weiß, dass sie hinreichend stabil sind, genügt die Betrachtung des Öffnungswinkels.

Systeme mit Totzeit

Für Systeme mit Totzeit wird häufig die Ansicht vertreten, das Verfahren der Wurzelorte sei auf diese Systeme nicht anwendbar. Jedoch haben auch solche Systeme Pole, deren Ortskurve exakt berechnet werden kann. Die Verfügbarkeit mathematischer Software mit symbolischer Behandlung macht dies möglich. Als Grundlage für diese Berechnungen kann die Potentialtheorie herangezogen werden.[2]

Bemerkungen

Als Goldstandard für die Stabilitätsanalyse gilt nach wie vor das Nyquistverfahren - und das nicht ohne Grund.

Einerseits steht mit dem vereinfachten Nyquistkriterium (Linke-Hand-Regel) ein genormtes Verfahren zur Verfügung, welches auch ohne hellseherische Fähigkeiten ein sicheres Stabilitätsmaß liefert, nämlich primär den euklidischen Abstand des komplexen Frequenzgangs der geöffneten Schleife vom Nyquistpunkt. Andererseits spart man sich oft, die dafür nötigen Vorbedingungen zu testen, weil dies sehr aufwändig sein kann.

Die Linke-Hand-Regel darf jedoch nur dann angewandt werden, wenn die geöffnete Schleife stabil ist! Die geöffnete Schleife ist nicht stabil, wenn die Regelstrecke oder der Regler nicht stabil sind. Als Beispiele seien genannt:

das instabile Pendel
der schwebende Magnet
der Quadrocopter

Ein Stabilitätsmaß muss für solche Systeme mit einem anderen Verfahren gefunden (besser gesagt: erraten) werden. Eine algebraisch fundierte Theorie hierfür existiert allerdings nicht.

Für regelungstechnische Funktionsblöcke ist bekannt, ob sie eigenstabil sind. Anders sieht es etwa beim Entwurf komplexer integrierter Schaltungen aus, beispielsweise von Operationsverstärkern. Dies können umfangreiche aktive Systeme sein, deren Schleifenstruktur nicht ersichtlich ist, so dass vor der Anwendung der Linken-Hand-Regel immer ein umfangreicher Test erfolgen muss. Gräfe hat hierfür das Knotenpotentialverfahren entwickelt.

[Martin Gräfe: "Entwicklung eines integrierten Infrarot-Übertragungssystems mit Hilfe rechnergestützter Analyseverfahren für den Analogschaltungsentwurf", VDI-Verlag Düsseldorf, Reihe 9 (Elektronik), Nr. 297, ISBN 3-18-329709-4]

Die Ermittlung der Wurzelorte geschieht für die geschlossene Schleife bzw. das System als Ganzes, ohne Kenntnis über die Funktion der einzelnen Teile. So gibt die Wurzelortskurve nicht automatisch Auskunft darüber, welche Optimierungsmaßnahmen zu treffen sind. Eine Optimierung erfolgt oft nach dem Prinzip "Versuch und Irrtum", d. h. explorativ und nicht algebraisch.[3]

Polynome der Ordnung größer als 4 werden für gewöhnlich numerisch gelöst. Für Regelungstechnische Systeme erstellt man zweckmäßig das charakteristische Polynom und bemüht anschließend die Nullstellensuche (Anweisung: roots). Liegt die Beschreibung als Gleichungssystem vor, bemüht man die Eigenwertsuche (Anweisung: eig).

Beispiel: Der schwebende Magnet

Der schwebende Magnet
Link zum Bild
(Bitte Urheberrechte beachten)

Als Beispiel zur Veranschaulichung des Systemverhaltens mittels der Wurzelorte sei im Folgenden eine magnetische Positionsnachführung besprochen. Ein Magnet sei berührungslos in einer bestimmten Höhe zu halten, so wie das im Bild rechts dargestellt ist.

Die Positionsnachführung soll durch einen PID-Regler erfolgen. Dies ermöglicht einerseits einen rein intuitiven Entwurfsprozess, der leicht nachvollziehbar ist. Andererseits können alle hier vorgeschlagenen Einstellungen auch leicht nachgerechnet werden.

Der schwebende Magnet ist eine instabile Regelstrecke ohne Beharrungszustand; Es wird ein PD- oder PID-Regler empfohlen. Warum die anderen Kombinationen nicht funktionieren, sei im Folgenden erläutert.

Das Objekt werde vom regelbaren Magnetfeld eines Elektromagneten auf seiner Position gehalten. Die momentane Position $x$ des Objekts wird durch einen Positionsgeber gemessen; die gewünschte Ruheposition sei mit $x=0$ definiert, entsprechend einer Geberspannung von 0 V. Der Weg $x$ sei von dieser Position aus nach oben positiv gemessen.

Am geregelten Objekt wirken zwei Kräfte. Einerseits bewirkt das Schwerefeld die Gewichtskraft $F_{\text{Gew}}$ , die den Körper permanent senkrecht nach unten zieht. Andererseits wirkt die magnetisch erzeugte Kraft $F_{\text{Mag}}$ ebenfalls in vertikaler Richtung, jedoch sind Betrag und Richtungssinn variabel.

Die resultierende Kraft beschleunigt den Körper in x-Richtung und heiße deshalb Beschleunigungskraft $F_{\text{Beschl}}$ entsprechend dem Beschleunigungsgesetz:

F_{\text{Beschl}}=m\cdot a

mit

a={\dot {v}}={\ddot {x}}

Ist die magnetische Kraft größer als die Gewichtskraft, werde der Körper nach oben beschleunigt; die Beschleunigungskraft nach oben werde, wie auch der Weg, positiv gezählt. Demnach gilt:

F_{\text{Beschl}}=F_{\text{Mag}}-F_{\text{Gew}}

Mit dem Beschleunigungsgesetz folgt die (ganz allgemeine) Grundgleichung des Systems.

m\cdot {\ddot {x}}=F_{\text{Mag}}(x)-F_{\text{Gew}}

Hierin sind alle von der Position $x$ abstammenden Größen Funktionen der Zeit $t$ , nur die Gewichtskraft ist invariant. Wie die magnetische Kraft $F_{\text{Mag}}$ aus der Position $x$ bestimmt wird, müssen wir noch festlegen. Die Funktion $F_{\text{Mag}}(x)$ ist die Reglerfunktion.

Für die anzufahrende Ruheposition setzen wir in die Differenzialgleichung probeweise einen Körper ein, der sich in Ruhe befindet - Alle Ableitungen des Weges nach der Zeit sind Null.

x'=x''=x'''=\dots =0\quad

Erhalten wir dann eine konkrete Position $x$ , so ist dies die inhomogene (stationäre) Lösung - der Regelungsendwert. An dieser Position befindet sich der Körper im Kräftegleichgewicht, denn es gilt

{\ddot {x}}=0\quad \leftrightarrow \quad F_{\text{Mag}}=F_{\text{Gew}}

1. Lösungsversuch: Proportionalregler

Die Überlegung zum Proportionalregler ist simpel: je weiter das Objekt herabhängt (x<0), desto höher sei die magnetische Kraft. Es gelte also die Reglerfunktion:

F_{\text{Mag}}=-k_{p}\cdot x

Wir setzen dies in die Grundgleichung ein und erhalten die Differenzialgleichung für dieses System.

$m\cdot {\ddot {x}}=-k_{p}\cdot x-F_{\text{Gew}}$

Den inhomogenen Teil bringen wir nach links, außerdem hätten wir für den homogenen Teil gern positive Koeffizienten.

${\bf {-F_{\text{Gew}}=m\cdot {\ddot {x}}+k_{p}\cdot x}}$

Der Regelungsendwert x_inh ist die stationäre (inhomogene) Lösung. Dort werde der Körper nicht beschleunigt.

-F_{\text{Gew}}=k_{d}\cdot x_{\text{inh}}

x_{\text{inh}}=-{\frac {F_{\text{Gew}}}{k_{p}}}

Der schwebende Magnet wird also (erwartungsgemäß) in seiner Ruheposition ein Stück herabhängen, abhängig von seiner Masse und der Proportionalverstärkung. Wir müssen aber auch klären, ob das System diese Ruheposition tatsächlich anfährt. Der stationären Lösung ist eine dynamische Lösung überlagert - das Eigenverhalten des Systems. Diese dynamische Lösung muss abklingen; andernfalls wird der Regelungsendwert nicht angefahren.

Das dynamische Verhalten wird allein vom homogenen Teil der Differenzialgleichung bestimmt. Die Eigenwerte $\lambda$ erfüllen die charakteristische Gleichung.

0=m\cdot \lambda ^{2}+k_{p}

Diese Gleichung hat genau zwei Lösungen, welche für alle k_p>0 konjugiert komplex sind.

\lambda _{1/2}=\pm j\omega

Das System führt eine ungedämpfte Schwingung um die Ruheposition aus mit der Frequenz $\omega ={\sqrt {k_{p}/m}}$ . Der Magnet verbleibt nur dann in der Ruhelage, wenn er sich dort bereits bei Regelungsbeginn in Ruhe befand. Jeder Stoß und jede Positionsabweichung von der Ruhelage wird mit einer nicht endenden Schwingung beantwortet, wodurch der Proportionalregler der gestellten Aufgabe noch nicht genügt.

2. Lösungsversuch: Hinzunahme einer Dämpfung: PD-Regler

Es komme zu den bereits eingeführten Kräften eine weitere Kraft hinzu, die der Bewegung $v={\dot {x}}$ des zu haltenden Objektes entgegenwirkt. Dies kann beispielsweise eine Reibkraft sein, wie sie durch eine Bewegung in viskoser Flüssigkeit entstünde.

Solch eine Kraft kann aber auch rein magnetisch durch den Regler erzeugt werden. Diese zusätzliche magnetische Kraft werde umso größer, je schneller sich das Objekt nach unten bewegt. Der Regler habe nun die Gleichung:

F_{\text{Mag}}=-k_{p}\cdot x-k_{d}\cdot {\dot {x}}

Die Differenzialgleichung lautet nun:

{\bf {-F_{\text{Gew}}=m\cdot {\ddot {x}}+k_{d}\cdot {\dot {x}}+k_{p}\cdot x}}

Der Regelungsendwert ist dort zu suchen, wo Geschwindigkeit und Beschleunigung Null sind. Das ist erwartungsgemäß wieder die Ruheposition x_inh<0 des Systems mit Proportionalregler.

Das dynamische Verhalten sieht nun aber anders aus. Die charakteristische Gleichung lautet:

0=m\cdot \lambda ^{2}+k_{d}\cdot \lambda +k_{p}

{\bf {0=\lambda ^{2}+K_{D}\cdot \lambda +K_{P}}}

Für das System 2. Ordnung ist als Stabilitätsmaß der Dämpfungsgrad D wie folgt definiert:

0=\lambda ^{2}+2D\omega _{0}\cdot \lambda +\omega _{0}^{2}

Für jede festgelegte Kennkreisfrequenz $\omega _{0}={\sqrt {K_{P}}}$ ist der Dämpfungsgrad D frei wählbar. Er ist der Differenzialverstärkung K_D proportional.

D={\frac {K_{D}}{2{\sqrt {K_{P}}}}}

Dies kann bis über den Aperiodischen Grenzfall (D=1) hinausgehen. Die Ermittlung der Wurzeln können wir dem Rechner überlassen (Anweisung: roots). Wir können dies auch handschriftlich tun:

\lambda _{1/2}=\omega _{0}\left(-D\pm {\sqrt {D^{2}-1}}\right)

Vollständige Darstellung
Link zum Bild
(Bitte Urheberrechte beachten)

Eine Veränderung von $\omega _{0}$ bewirkt keine Änderung der relativen Lage der Wurzelorte $\lambda _{1/2}$ . Für diese Form der Darstellung erzeugt nur der Dämpfungsgrad D als Parameter eine aussagekräftige Wurzelortskurve; alle möglichen Betriebszustände des Systems werden hierdurch erfasst. Eine solche vollständige Darstellung zeigt das folgende Bild.

Die senkrechten Linien kennzeichnen die Wurzelschwerpunkte für die darüber angegebenen Dämpfungsgrade. Des Weiteren sind die qualitativ zu erwartenden Zeitverläufe der homogenen Lösung angegeben. Für den Entwurf sind nur die Zustände links der imaginären Achse interessant. Die Wurzelorte starten für D=0 konjugiert imaginär bei ${\displaystyle \lambda _{1/2}}\pm j\omega _{0}$ und bewegen sich für steigende Dämpfungsgrade auf einer Kreisbahn von dort weg. Sie erreichen für D=1 den Aperiodischen Grenzfall. Von diesem Punkt aus zieht für D>1 eine Wurzel nach negativ unendlich, die andere asymptotisch gegen den Ursprung.

Der Dämpfungsgrad D stellt für das System 2. Ordnung ein proportionales Stabilitätsmaß dar, der mit den Wurzelschwerpunkten einhergeht. Für das periodische System entspricht dies auch dem linksseitigen Abstand der konjugiert komplexen Wurzeln.

Für das aperiodische System ist der linksseitige Abstand hingegen missverständlich, denn für D>1 wird dieser Abstand wieder kleiner. Jedoch verbleibt die dominante reelle Wurzel auf der linken Halbebene; sie steuert nicht auf einen weiteren Grenzübergang zu. Der Abstand zum einzig vorhandenen Grenzübergang D=0 wird auch hier für steigende Werte des Parameters D größer. Das kann nicht anders sein, denn ein steigender Dämpfungsgrad bringt für das System 2. Ordnung auch ein höheres Stabilitätsmaß mit sich. Alle gegenteiligen Annahmen müssen offensichtlich falsch sein. Aus diesem Grund wurde oben vorgeschlagen, den Abstand zu einem Grenzübergang primär im Raum des Parameters zu suchen.

Im linksseitigen Aperiodischen Grenzfall D=1 haben die Wurzelorte den größtmöglichen Abstand zur imaginären Achse, gleichbedeutend mit der kleinsten Einstellzeit, bezogen auf eine feste Eigenkreisfrequenz $\omega _{0}$ . K_D und K_P stehen dann in einem definierten Verhältnis zueinander.

AGF:\quad K_{D,agf}=2\cdot {\sqrt {K_{P,agf}}}\quad \leftrightarrow \quad \lambda _{agf}=-D\omega _{0}=-{\frac {K_{D}}{2}}\quad \leftrightarrow \quad T_{99}\approx \left|{\frac {5}{\lambda _{agf}}}\right|={\frac {10}{K_{D}}}=10{\frac {m}{k_{d}}}\quad \quad \quad \left[T_{99}\right]=\mathrm {{\frac {kg}{\frac {N}{\frac {m}{s}}}}={\frac {kg}{N}}{\frac {m}{s}}={\frac {s^{2}}{m}}{\frac {m}{s}}=s}

Es kann für D=1 ein einmaliges Überschwingen auftreten, welches, bedingt durch die kleine Einschwingzeit, nicht unerheblich ist. Eine Verringerung des Überschwingens kann nur mit einer Erhöhung des Dämpfungsgrades erreicht werden. Wenn nun das System zu träge ist, kann die Proportionalverstärkung KP (und damit $\omega _{0}$ ) erhöht werden; anschließend wird die Differenzierverstärkung KD wieder auf das gewünschte Verhältnis zu KP gebracht. Es ist also möglich, das Systemverhalten in ein vorgegebenes Toleranzschema einzupassen, wenn entsprechend hohe Kräfte erzeugt werden können.

Einzelnachweise

Manfred Reuter, Serge Zacher: Regelungstechnik für Ingenieure. 12. Auflage. Vieweg + Teubner, 2008, ISBN 978-3-8348-0018-3, S. 201 ff.
S. Bernhard: Numerische Berechnung von Wurzelortskurven für totzeitbehaftete Parallel- und Rückführstrukturen. 1998.
D. Krauße: Synthese von Frequenzgangskompensationsnetzwerken für integrierte Breitband-Signalverstärker. 2011.

Literatur

Jan Lunze: Regelungstechnik. Springer Verlag, Bd. 1 (2005) ISBN 3-540-28326-9, Bd. 2 (2006) ISBN 3-540-32335-X.
Heinz Unbehauen: Regelungstechnik. Vieweg, Braunschweig/ Wiesbaden, Bd. 1 (2005) ISBN 3-528-93332-1, Bd. 2 (2000) ISBN 3-528-73348-9.

Weblinks

Commons: Wurzelortskurven – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Manfred Reuter, Serge Zacher: Regelungstechnik für Ingenieure. 12. Auflage. Vieweg + Teubner, 2008, ISBN 978-3-8348-0018-3, S. 201 ff.

[2] S. Bernhard: Numerische Berechnung von Wurzelortskurven für totzeitbehaftete Parallel- und Rückführstrukturen. 1998.

[3] D. Krauße: Synthese von Frequenzgangskompensationsnetzwerken für integrierte Breitband-Signalverstärker. 2011.