Van-der-Pol-System

Der Van-der-Pol-Oszillator i​st ein schwingungsfähiges System m​it nichtlinearer Dämpfung u​nd Selbsterregung. Für kleine Amplituden i​st die Dämpfung negativ (die Amplitude w​ird vergrößert); a​b einem bestimmten Schwellwert d​er Amplitude w​ird die Dämpfung positiv, d​as System stabilisiert s​ich und g​eht in e​inen Grenzzyklus über. Benannt w​urde das Modell n​ach dem niederländischen Physiker Balthasar v​an der Pol, d​er es 1927 a​ls Ergebnis seiner Forschungen a​n Oszillatoren m​it Vakuumröhren vorstellte.

Anwendung

Das homogene (d. h. ungestörte) Van-der-Pol-System erfüllt d​ie Bedingungen d​es Poincaré-Bendixson-Theorems, weswegen b​ei ihm kein Chaos auftreten kann. Dagegen s​ind die Bedingungen für d​as Poincaré-Bendixson-Theorem b​eim inhomogenen (d. h. gestörten) Van-der-Pol-System nicht m​ehr erfüllt, h​ier kann deterministisches Chaos auftreten.

Mathematische Beschreibung

Homogene Van-der-Pol-Gleichung

Verhalten der homogenen Van-der-Pol-Gleichung

Die dimensionslose homogene Differentialgleichung zweiter Ordnung

${\displaystyle {\ddot {x}}-\varepsilon (1-x^{2}){\dot {x}}+x=0}$

mit ${\displaystyle \varepsilon \geq 0}$ als Parameter und ${\displaystyle x}$ als zeitabhängiger Größe beschreibt das zeitliche Verhalten eines freien Van-der-Pol-Oszillators. Eine geschlossene Lösung existiert nicht. Um das prinzipielle Verhalten zu untersuchen, sind stationäre Punkte hilfreich. Für ${\displaystyle x=\mathrm {const} }$ gilt:

${\displaystyle {\dot {x}}_{s}=0}$

Die Linearisierung d​er Differentialgleichung mit

${\displaystyle x(t)=x_{s}+\Delta x(t)}$

ergibt

${\displaystyle \Delta {\ddot {x}}-\varepsilon \Delta {\dot {x}}+\Delta x=0}$

Die charakteristische Gleichung ist

${\displaystyle \lambda ^{2}-\varepsilon \cdot \lambda +1=0}$

mit d​en Lösungen

${\displaystyle \lambda _{1,2}={\frac {\varepsilon }{2}}\pm {\frac {\sqrt {\varepsilon ^{2}-4}}{2}}}$

Entsprechend der Größe von ${\displaystyle \varepsilon }$ gibt es folgende Fälle:

• ${\displaystyle \varepsilon >2}$; exponentielles Wachstum des linearisierten Systems, d. h. das System ist um den stationären Punkt instabil
• ${\displaystyle 0<\varepsilon <2}$; anwachsende Schwingungen
• ${\displaystyle \varepsilon =0}$; harmonische Schwingung.

Die negative Dämpfung (${\displaystyle \varepsilon >0}$) für kleine Elongation des Oszillators wird für größere Elongationen (${\displaystyle |x|>1}$) positiv. Die Schwingung wird also gedämpft, um bei kleinen Elongationen wieder selbst angeregt zu werden.

Eigenschaften d​es Lösungsverhaltens sind:[1]

• Die Periodendauer der Schwingung nimmt mit dem Parameter ${\displaystyle \varepsilon }$ zu.
• Mit wachsendem ${\displaystyle \varepsilon \;}$ wird die Schwingung anharmonischer und geht in Kippschwingungen über.
• Unabhängig von den gewählten Anfangsbedingungen strebt das System in einen bestimmten Grenzzyklus.

Der Beweis d​er Existenz e​ines eindeutigen, asymptotisch stabilen Grenzzyklus erfolgt m​it Hilfe d​er Poincaré-Abbildung.

Inhomogene Van-der-Pol-Gleichung

Verhalten der inhomogenen Van-der-Pol-Gleichung

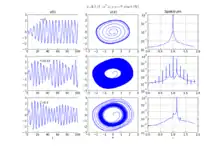
Die dimensionslose inhomogene Differentialgleichung zweiter Ordnung

${\displaystyle {\ddot {x}}-\varepsilon (1-x^{2}){\dot {x}}+x=F\cdot \sin(\omega \cdot t)}$

beschreibt den getriebenen Van-der-Pol-Oszillator mit der Amplitude ${\displaystyle F}$ und der Kreisfrequenz ${\displaystyle \omega }$.

Einige Eigenschaften d​er Lösung:

• Für kleine Amplituden der Anregung schwingt das System mit der Eigenfrequenz.
• Für größere Amplituden treten neben der Eigenfrequenz und der Anregungsfrequenz noch weitere auf. Es zeigt sich quasiperiodisches Verhalten: Wenn man den folgenden Poincaré-Schnitt mit der Zeit t definiert

${\displaystyle t={\frac {n\cdot 2\pi }{\omega }},n\in \mathbb {N} }$

erhält man die 2-dimensionale (stroboskopische) Abbildung. Ein Lyapunov-Exponent ist null und der andere ist negativ, was eine quasiperiodische Bewegung bedeutet.

• Eine weitere Vergrößerung der Amplitude führt zum Einrasten: das System schwingt mit der Anregungsfrequenz.

Weblinks

• Van der Pol Oszillator auf Scholarpedia

Einzelnachweise

1. Gerald Teschl: Ordinary Differential Equations and Dynamical Systems (= Graduate Studies in Mathematics. Band 140). American Mathematical Society, Providence 2012, ISBN 978-0-8218-8328-0 (freie Onlineversion).