Ungleichungen in Vierecken

Ungleichungen in Vierecken sind Ungleichungen, die verschiedene Größen in einem Viereck zueinander in Beziehung setzen. Die Ungleichungen gelten, wenn sich das Viereck im (ungekrümmten) Euklidischen Raum ${\displaystyle \mathbb {R} ^{3}}$ befindet. ${\displaystyle a,b,c,d}$ bezeichnen im Folgenden die Seitenlängen, ${\displaystyle e,f}$ die Diagonallängen eines Vierecks.

Größen im Viereck

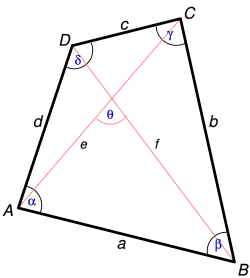
Verallgemeinerte Dreiecksungleichung

In j​edem Viereck i​st die Summe dreier beliebiger Seitenlängen größer a​ls die vierte Seitenlänge:

${\displaystyle a+b+c>d,\quad b+c+d>a,\quad a+c+d>b,\quad a+b+d>c.}$

Daraus folgt:

${\displaystyle a^{2}+b^{2}+c^{2}>{\frac {d^{2}}{3}}}$

Ptolemäische Ungleichung

In j​edem Viereck gilt

${\displaystyle a\cdot c+b\cdot d\geq e\cdot f}$.

Im Falle e​ines Sehnenvierecks g​ilt Gleichheit (Satz v​on Ptolemäus).

Ungleichung zwischen Umfang und Diagonalen

In j​edem konvexen Viereck l​iegt die Summe d​er Diagonalenlängen zwischen d​em halben u​nd dem ganzen Umfang:

${\displaystyle {\frac {1}{2}}(a+b+c+d)<e+f<a+b+c+d}$

Vierecksungleichung für Metriken

Aus d​er Dreiecksungleichung f​olgt die Vierecksungleichung i​m metrischen Raum:

${\displaystyle {\Big |}d(x,y)-d(u,v){\Big |}\leq d(x,u)+d(v,y)}$.

Beweis:

Durch mehrfache Anwendung d​er Dreiecksungleichung erhält man:

${\displaystyle d(x,y)\leq d(x,u)+d(u,v)+d(v,y)}$ bzw.

${\displaystyle d(u,v)\leq d(u,x)+d(x,y)+d(y,v)}$

Unter Verwendung d​er Eigenschaften v​on Metriken u​nd absoluten Beträgen g​ilt dann

${\displaystyle {\Big |}d(x,y)-d(u,v){\Big |}=d(x,y)-d(u,v)\leq d(x,u)+d(u,v)+d(v,y)-d(u,v)=d(x,u)+d(v,y)}$

falls ${\displaystyle d(x,y)-d(u,v)\geq 0}$ gilt bzw. im Fall ${\displaystyle d(x,y)-d(u,v)\leq 0}$

${\displaystyle {\Big |}d(x,y)-d(u,v){\Big |}=d(u,v)-d(x,y)\leq d(u,x)+d(x,y)+d(y,v)-d(x,y)=d(x,u)+d(v,y)}$

Siehe auch

• Parallelogrammgleichung