Triangulation (Fläche)
Unter Triangulation oder Triangulierung einer Fläche versteht man
- a) ein Netz von Dreiecken im Raum, das auf einer vorgegebenen Fläche liegt und diese teilweise oder vollständig überdeckt, oder
- b) die Prozedur der Erzeugung der Punkte und Dreiecke eines solchen Dreiecks-Netzes.
Hier wird ausschließlich die Erzeugung eines Dreiecksnetzes beschrieben. In der Literatur gibt es Beiträge, die sich mit der Optimierung eines vorhandenen Netzes beschäftigen.
Triangulationen sind ein wichtiges Hilfsmittel bei
- der Visualisierung von Flächen und
- der Anwendung von Finite-Elemente-Methoden.
Die Triangulation einer parametrisierten Fläche kann man durch eine Triangulierung ihres Definitionsbereichs erhalten (s. 2. Bild). Aber die Bilder dieser Dreiecke können im Objektraum sehr verschieden in Gestalt und Größe ausfallen, was ihre Verwendung einschränken kann. Diesen Mangel kann man mit adaptiven Methoden verringern. Dabei werden 3D-Informationen (Schrittweiten) zur Triangulierung des Parameterbereichs verwendet.
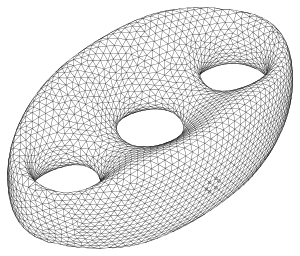
Die Triangulierung einer implizit gegebenen Fläche (durch eine oder mehrere Gleichungen bestimmte Fläche) ist wesentlich schwieriger. Die meisten Algorithmen unterteilen den zu betrachtenden Bereich (im Raum) in Quader und approximieren den Schnitt der Fläche mit diesen Quadern durch Polygone, die dann noch trianguliert werden müssen (cutting cube method).[1][2] Der Aufwand dieser Algorithmen zur Verwaltung der Daten ist erheblich. Ein vom Konzept her einfacherer Algorithmus, der Verfolgungs-Algorithmus (marching method),[3][4][5] erzeugt von einem Startpunkt ausgehend zunächst ein Sechseck von näherungsweise gleichseitigen Dreiecken und fügt schrittweise nach vorgegebenen Regeln immer wieder neue Dreiecke hinzu, bis der zur Triangulation vorgesehene Bereich der Fläche trianguliert ist. Bei Flächen mit mehreren Zusammenhangskomponenten muss der Verfolgungsalgorithmus allerdings entsprechend oft mit geeigneten Startpunkten durchlaufen werden, was bei dem cutting cube Algorithmus nicht der Fall ist. D. h. beim Verfolgungsalgorithmus muss man schon eine gewisse Vorstellung von der zu triangulierenden Fläche haben, was in der Regel der Fall ist. Der cutting cube Algorithmus entdeckt bei entsprechenden Vorgaben für die Unterteilungstiefe automatisch alle Komponenten der Fläche in dem vorgegebenen Ausgangswürfel. Ein weiterer Vorteil des Verfolgungs-Algorithmus besteht in der Möglichkeit Begrenzungskurven vorzugeben (s. Beispiel).
Polygonalisierung von Flächen wird in der weitgehend englischen Literatur meshing genannt. Die Erzeugung von 4-Ecksnetzen heißt dort paving.
Die Triangulierung einer Fläche sollte nicht verwechselt werden mit der Triangulierung einer vorgegebenen diskreten ebenen Punktmenge. Siehe Delaunay-Triangulation.
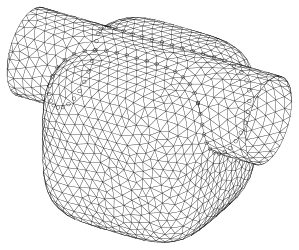Triangulation: Zylinder, Fläche
Triangulation: Zylinder, Fläche , povray-Bild
Torus: mit Verfolgungsalgorithmus trianguliert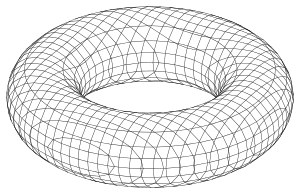
Torus: cutting cube Methode, polygonisiert
Siehe auch
Einzelnachweise
- M. Schmidt: Cutting Cubes - visualizing implicit surfaces by adaptive polygonization. Visual Computer (1993) 10, S. 101–115
- J. Bloomenthal: Polygonization of implicit surfaces, Computer Aided Geometric Design (1988), S. 341–355
- CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt) (PDF; 3,4 MB), S. 187
- E. Hartmann: A marching method for the triangulation of surfaces, The Visual Computer (1998), 14, S. 95–108
- S. Akkouche & E Galin: Adaptive Implicit Surface Polygonization Using Marching Triangles, COMPUTER GRAPHICS forum (2001), Vol. 20, S. 67–80
Weblinks
- E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN, S. 81
- Tasso Karkanis & A. James Stewart: Curvature-Dependent Triangulation of Implicit Surfaces