Translationsinvariante Funktion

Als translationsinvariant werden in der Mathematik Abbildungen bezeichnet, deren Wert sich unter einer Translation nicht ändert. Genauer heißt ein Funktional $F(f)\to \mathbb {R}$ translationsinvariant, wenn sich der Wert des Funktionals nicht ändert, wenn die Funktion $f\colon \mathbb {R} ^{n}\to \mathbb {R}$ einer Translation mit Verschiebungsvektor $a\in \mathbb {R} ^{n}$ unterzogen wird: $Tf(x)=f(x-a)$ .

Für translationsinvariante Funktionen

f\colon \mathbb {R} ^{2}\rightarrow \mathbb {R}

ist

f(A)=f(A+t)

. Dies gilt beispielsweise für das Lebesgue-Maß.

Die Kleiner-Relation auf den reellen Zahlen ist translationsinvariant.

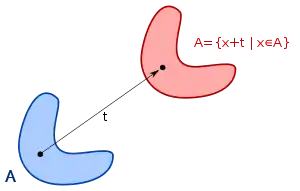
Beispielsweise ist jede konstante Funktion translationsinvariant. Ein anderes Beispiel ist das Lebesgue-Integral. Anschaulich bedeutet dessen Translationsinvarianz, dass sich der Wert eines Integrals nicht ändert, wenn der Definitionsbereich verschoben wird, genauso wie sich das Volumen eines Körpers nicht durch reine Verschiebung im Raum ändert.

Da eine Translation ein Spezialfall einer Bewegung, ist auch jede translationsinvariante Funktion eine bewegungsinvariante Funktion.

Allgemeine Definition: Translationsinvarianz in Gruppen

Allgemeiner ist es möglich, Translationsinvarianz bei Gruppenoperationen zu definieren. Sei X eine Menge mit einer transitiven Operation einer Gruppe G. Dann induziert

x\to gx

für jedes Element g von G einen Automorphismus von X und damit einen Automorphismus auf jeder funktoriellen Konstruktion F(X) auf X. Die G-Invarianten in F(X) werden translationsinvariant genannt.

Für eine Gruppe G und X=G kann man durch

h\to gh

und

h\to hg^{-1}

zwei G-Räume definieren, die zugehörige Translationsinvarianz wird Links- bzw. Rechtsinvarianz genannt.

Beispielsweise ist die Lie-Algebra einer Lie-Gruppe der Raum der linksinvarianten Vektorfelder. Ein Haar-Maß auf einer topologischen Gruppe ist ebenfalls translationsinvariant. Das Petersson-Skalarprodukt auf der oberen Halbebene wird mit Hilfe eines SL(2,R)-invarianten Maßes definiert.

Sonstiges

Translationsinvariant ist auch eine stochastische Funktion, die nur um additive (oder subtraktive) Komponenten verändert wird. Hierbei werden die Gesetzmäßigkeiten, die mit der Funktion beschrieben werden, nicht berührt. Nur die Mittel- bzw. Skalenwerte verändern sich.

Literatur

Otto Forster: Analysis. Band 3: Maß- und Integrationstheorie, Integralsätze im Rⁿ und Anwendungen, 8. verbesserte Auflage. Springer Spektrum, Wiesbaden, 2017, ISBN 978-3-658-16745-5.
Konrad Königsberger: Analysis 2, Springer, Berlin 2004.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.