Trägheitsradius
Der Trägheitsradius ist derjenige Abstand von der gegebenen Drehachse, in dem man die punktförmig gedachte Masse m des Körpers anbringen muss, um das Trägheitsmoment J zu erhalten.[1]
Für eine gute Materialausnutzung z. B. bei Schwungrädern wird ein Trägheitsradius angestrebt, der im Vergleich zur Außenabmessung groß ist, d. h. möglichst weit außen liegt.
In der Festigkeitslehre gilt ein analoger Zusammenhang zwischen der Fläche A und dem Flächenmoment zweiten Grades I:
Der Trägheitsradius geht hier als Berechnungsgröße in den Nachweis von Knicklasten ein.
Berechnung des Trägheitsradiuses bei bekannter Geometrie
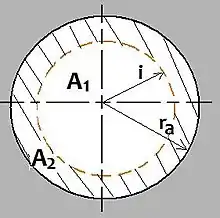
Zylinder: , ,
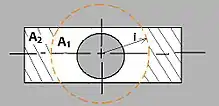
beliebiger Querschnitt:
-> Aus dieser Gleichung lässt sich jeweils der Trägheitsradius errechnen.
Polymerchemie
In der Polymerchemie wird der mittlere quadratische Abstand der Molekülketten vom Schwerpunkt des Moleküls als Streumassenradius bezeichnet, teilweise auch als Trägheitsradius.[2]
Literatur
- Martin Mayr: Technische Mechanik: Statik – Kinematik – Kinetik – Schwingungen – Festigkeitslehre. Teil 3, ISBN 978-3-446-22608-1, Kap. 5.
Einzelnachweise
- Alfred Böge (Hrsg.): Vieweg Handbuch Maschinenbau: Grundlagen und Anwendungen der Maschinenbau-Technik. 18. Auflage. Vieweg, 2007, ISBN 978-3-8348-0110-4 (eingeschränkte Vorschau in der Google-Buchsuche).
- Friedrich R. Schwarzl: Polymermechanik: Struktur und mechanisches Verhalten von Polymeren. Springer, 1990, ISBN 3-540-51965-3 (eingeschränkte Vorschau in der Google-Buchsuche).
Weblinks
- Festigkeitslehre (abgerufen am 18. Oktober 2019)
- Flächenträgheitsmomente (abgerufen am 18. Oktober 2019)
- Fakultät für Physik und Geowissenschaften Physikalisches Grundpraktikum (abgerufen am 18. Oktober 2019)
- Tragfähigkeit von Stäben aus Baustahl – Nichtlineares Tragverhalten, Stabilität, Nachweisverfahren (abgerufen am 18. Oktober 2019)