Thorndike-Nomogramm
Das Thorndike-Nomogramm ist ein zweidimensionales Diagramm der Poisson-Verteilung. In diesem Nomogramm lassen sich die Werte der Verteilungsfunktion (dies ist die Wahrscheinlichkeitssumme) auf graphischem Weg näherungsweise ermitteln. Es ist benannt nach Frances Thorndike, die dieses Nomogramm 1926 entwickelte. Im Oktober 1926 wurde das Thorndike-Nomogramm veröffentlicht unter dem Titel „Application of Poisson’s Probability Summation“.[1]
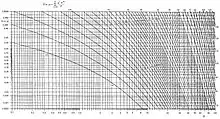
Praktische Bedeutung
Die wichtigsten Anwendungen des Thorndike-Nomogramms liegen in der Qualitätssicherung. Vor allem in der industriellen Serienproduktion stellt das Thorndike-Nomogramm ein wichtiges Hilfsmittel zur Beurteilung der Qualitätslage, für die Stichprobentechnik und für die Regelkartentechnik dar. Das Thorndike-Nomogramm ermöglicht einfache Lösungswege zu Problemstellungen der Art „Anzahl von Fehlern pro Einheit“. Eine typische Problemstellung dieser Art wäre etwa die Anzahl Lötfehler pro Fernsehgerät. Weniger bekannt ist, dass solche Problemstellungen auch außerhalb von Technik oder Industrie oft vorkommen, beispielsweise Anzahl Astlöcher pro Tischplatte oder Anzahl Pigmentflecken pro Patient.
Vor- und Nachteile
Der Vorteil des Thorndike-Nomogramms besteht darin, dass man zu seiner Benutzung kein Mathematiker sein muss, man muss auch keine besonderen theoretischen Kenntnisse der Statistik besitzen. Nur mit dem auf Papier gedruckten Nomogramm (oder einer Fotokopie) plus Bleistift und Lineal lassen sich sehr leicht in wenigen Sekunden Ergebnisse erzielen. Ein kleiner Nachteil besteht darin, dass die Ergebnisse nur eine näherungsweise Genauigkeit haben – die geringen Abweichungen von den mathematisch exakten Werten haben aber für die Praxis meistens keine Bedeutung.
Alternativen
- Für kleine Zahlen lässt sich die Poisson-Verteilung auf dem Formelweg berechnen.
- Bei größeren Zahlen kann man Taschenrechner oder noch besser programmierbare Taschenrechner benutzen.
- Die Werte lassen sich aus bestimmten statistischen Tabellen ablesen.
- Es gibt spezielle Computerprogramme zur Berechnung der Poisson-Verteilung.
Formelzeichen im Thorndike-Nomogramm
Die in der Qualitätssicherung verwendeten Formelzeichen unterscheiden sich teilweise von den Formelzeichen in mathematischen Fachbüchern. In der Qualitätssicherung ist die folgende Schreibweise üblich:
- Die Verteilungsfunktion hat das Formelzeichen G. Der besser verständliche Name der Verteilungsfunktion lautet Wahrscheinlichkeitssumme – dies ist die Wahrscheinlichkeit, in einer Stichprobe bis zu x Fehler zu finden. Die Bezeichnung „bis zu x Fehler“ wird klarer, wenn man sich vorstellt, dass z. B. bis zu 2 Astlöcher in einer Tischplatte noch zulässig wären. Den Möbelfachmann interessiert dann nicht die Wahrscheinlichkeit, dass genau 2 Astlöcher in der Tischplatte sind – ihn interessiert die Wahrscheinlichkeit, dass bis zu 2 Astlöcher in der Tischplatte sind und diese ist gleich der Summe der Wahrscheinlichkeiten für 0 Astlöcher, für 1 Astloch und für 2 Astlöcher – eben bis zu 2. Die Zahlenwerte der Verteilungsfunktion G lassen sich auf der Skala am linken Rand des Thorndike-Nomogramms ablesen. Achtung: Die Skala ist nicht in Prozent (%) dargestellt. Eine Wahrscheinlichkeitssumme von 1 % ergibt auf der Skala den Wert 0,01.
- Der Erwartungswert für die Anzahl von Fehlern in der Stichprobe hat das Formelzeichen µ. Ein anderer Ausdruck für diesen Erwartungswert ist die „mittlere Anzahl von Fehlern pro Stichprobe“. Die Skala für µ befindet sich am unteren Rand des Thorndike-Nomogramms. Die Skala für die mittlere Anzahl von Fehlern in der Stichprobe µ reicht bei den meisten Thorndike-Nomogrammen von 0,2 bis 30.
- Die Anzahl von Fehlern in der Stichprobe hat das Formelzeichen x. Die Anzahl von Fehlern in der Stichprobe kann logischerweise nur natürliche Zahlen (einschließlich der Null) annehmen. Bis x = 20 ist für jeden x-Wert eine Linie im Thorndike-Nomogramm vorhanden. Ab x = 20 in Zweierschritten, später in noch größeren Schritten. Achtung: die x-Werte stehen unter den Linien!
Funktionsweise
Man nehme
- Gedrucktes oder kopiertes Thorndike-Nomogramm
- Durchsichtiges Lineal, Länge ca. 25 cm
- Spitzer Bleistift HB
- Radiergummi für Korrekturen
- Beleuchtung von vorn/ oben
- Man markiert den µ-Wert auf der Skala am unteren Rand des Thorndike-Nomogramms
- Man zeichnet mit dem Bleistift eine dünne, gerade Linie vom µ-Wert senkrecht bis zu der Linie des gegebenen x-Wertes
- Von dem Schnittpunkt der Bleistiftlinie mit der x-Linie zeichnet man eine dünne Bleistiftlinie waagerecht nach links bis zur G-Skala.
- Am Schnittpunkt mit der G-Skala kann man den Wert der Verteilungsfunktion, also die Wahrscheinlichkeitssumme ablesen.