Tübinger Dreieck

Das Tübinger Dreieck ist neben der Penrose-Rauten-Parkettierung und deren Variationen ein klassischer Kandidat, um Quasikristalle fünffach oder zehnfach zu modellieren.

Tübinger Dreieck

Tübinger Dreiecke

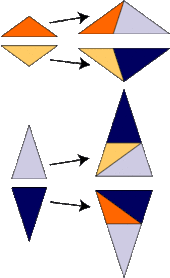
Der Inflationsfaktor ist, wie im Falle der Penrose-Raute, der Goldene Schnitt: $\Phi ={\frac {a}{b}}={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618.$

Die Prototeilungen sind Robinson-Dreiecke, aber ihre Teilungen sind anders als bei den Penrose-Rauten: Die Penrose-Rauten lassen sich von den Tübinger Dreiecken ableiten. Die Tübinger Dreiecke wurden von einer Gruppe von Tübinger Wissenschaftlern entdeckt und studiert. Daher stammt ihr Name. Da die Prototeilungen spiegelsymmetrisch aufgebaut sind, aber ihre Substitutionen nicht, muss man rechtshändige und linkshändige Versionen unterscheiden. Dies wird durch die Farben der Substitutionsregelung in den Bildern dargestellt.[1][2]

Einzelnachweise

E. Harriss (Zeichnungen), D. Frettlöh (Text): Tuebingen Triangle. (Memento des Originals vom 2. April 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Abgerufen am 5. März 2014.
M. Baake, P. Kramer, M. Schlottmann, D. Zeidler: Planar patterns with fivefold symmetry as sections of periodic structures in 4-space. In: International Journal of Modern Physics B. Band 04, 15n16, Dezember 1990, S. 2217–2268, doi:10.1142/S0217979290001054.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] E. Harriss (Zeichnungen), D. Frettlöh (Text): Tuebingen Triangle. (Memento des Originals vom 2. April 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Abgerufen am 5. März 2014.

[2] M. Baake, P. Kramer, M. Schlottmann, D. Zeidler: Planar patterns with fivefold symmetry as sections of periodic structures in 4-space. In: International Journal of Modern Physics B. Band 04, 15n16, Dezember 1990, S. 2217–2268, doi:10.1142/S0217979290001054.