Suriza
Suriza (japanisch スリザーリンク surizā rinku, englisch slither link) ist ein Rätsel, das zuerst von der japanischen Zeitschrift Nikoli veröffentlicht wurde.

Suriza ist auch noch unter anderen Namen bekannt, dazu gehören Schlangenlinie, Slitherlink, Heiliger Pfad, Rundweg, Gartenzaun, Fences und Number line.
Regeln
Suriza wird auf einem Quadratgitter gespielt. Die Gitterpunkte und die Kanten sind dabei meist markiert oder hervorgehoben. Ziel ist es, einen geschlossenen Weg ohne Kreuzungen und Verzweigungen aus Kanten zwischen den Punkten des Gitters zu zeichnen. Dabei stehen in manchen Quadraten Zahlen zwischen 0 und 3, die angeben, wie viele Kanten des Weges an dieses Feld angrenzen müssen. Nicht markierte Felder können eine beliebige Zahl von 0 bis 3 enthalten und somit können auch beliebig viele Kanten des Weges an diesen Feldern anliegen.
Normalerweise wird die Lösung bzw. der gesuchte Weg eindeutig durch die vorgegebenen Zahlen festgelegt.
Lösungsstrategie
Zur Lösung einer Suriza versucht man typischerweise zuerst kleine Fragmente des gesuchten Weges zu bestimmen, die sich dann nach und nach zu größeren Teilstücken verbinden lassen. So muss beispielsweise zwischen zwei Feldern, die beide eine Drei beinhalten, ein Stück des gesuchten Weges liegen. Durch logische Überlegungen lassen sich so noch weitere Regeln finden.
Am besten versucht man Linien auszuschließen, auf denen der Weg nicht liegen kann. Alle nicht ausgeschlossenen Linien bilden dann den Weg.
Genau 2 oder 0 Linien an jedem Kreuzungspunkt
Der Schlüssel zur Lösung von Suriza ist, dass sich an jedem Kreuzungspunkt genau 2 Linien treffen, oder gar keine. Man versucht einfach konsequent Linien auszuschließen. Konnte man irgendwo im Spielfeldinneren (nicht am Rand) drei Linien eines Punktes ausschließen, so muss zwangsläufig auch die vierte Linie dieses Punktes ausgeschlossen werden. Ein Punkt ist immer mit 2 oder 0 Linien verbunden, sonst kann man keinen durchgehenden Weg erhalten.
Desgleichen, wenn ein Punkt am Spielfeldrand (aber keine Ecke) bereits zwei Linien hat, welche ausgeschlossen werden konnten, so muss die dritte Linie ebenfalls ausgeschlossen werden. Für einen Eckpunkt gilt, wenn eine Linie ausgeschlossen werden konnte, so muss auch die verbleibende zweite Linie ausgeschlossen werden.
Die Anwendung dieser einfachen Ausschlussregeln führt zur Lösung aller Suriza-Puzzles.
Eckfelder
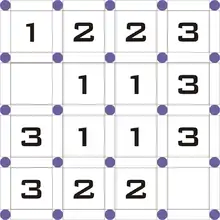
In dem Beispiel befindet sich in dem Eckfeld links oben eine 1. Es darf also nur eine der vier Kanten dieses Eckfeldes für den Weg benutzt werden. Das schließt automatisch die linke und die obere Kante aus. Ob nun die untere oder rechte Kante genutzt werden muss, ergibt sich erst später.
Im Eckfeld rechts oben steht eine 3. Die einzige Möglichkeit, drei Kanten zu benutzen ist, wenn die obere und die rechte Kante mit dabei sind. Also kann man diese bereits sicher als Teil des Weges markieren.
Befindet sich in einem Eckfeld jedoch eine 2, so kann man bezüglich der Kanten dieses Feldes keine Aussage treffen, außer dass zwei Kanten ‚über Eck‘ mit im Weg sind. Das führt jedoch dazu, dass man die beiden dahin führenden Kanten am Rand bereits als Teil des Weges markieren kann.
Randfelder
Im Beispiel befinden sich rechts oben drei Felder mit jeweils einer 3 direkt untereinander. Dort kann man direkt die vier horizontalen Kanten als Teil des Weges markieren.
Literatur
- Yukio Suzuki: Sudoku für Könner. 102 knifflige Zahlenrätsel – Das Kulträtsel auf Japan. Goldmann, München 2005, ISBN 3-442-16826-0, (Mosaik bei Goldmann 16826)