Subdifferential

Das Subdifferential i​st eine Verallgemeinerung d​es Gradienten a​uf nicht differenzierbare konvexe Funktionen. Das Subdifferential spielt e​ine wichtige Rolle i​n der konvexen Analysis s​owie der konvexen Optimierung.

Definition

Sei ${\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} }$ eine konvexe Funktion. Ein Vektor ${\displaystyle g\in \mathbb {R} ^{n}}$ heißt Subgradient von ${\displaystyle f}$ an der Stelle ${\displaystyle x_{0}}$, wenn für alle ${\displaystyle x\in \mathbb {R} ^{n}}$ gilt[1]

${\displaystyle f(x)\geq f(x_{0})+\langle g,x-x_{0}\rangle }$,

wobei ${\displaystyle \langle \cdot ,\cdot \rangle }$ das Standardskalarprodukt bezeichnet.

Das Subdifferential ${\displaystyle \partial f(x_{0})}$ ist die Menge aller Subgradienten von ${\displaystyle f}$ im Punkt ${\displaystyle x_{0}}$.[2]

Anschauung

Subgradienten einer konvexen Funktion

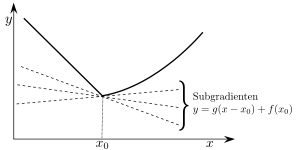
Intuitiv bedeutet diese Definition für ${\displaystyle n=1}$, dass der Graph der Funktion ${\displaystyle f}$ überall über der Geraden ${\displaystyle G}$ liegt, die durch den Punkt ${\displaystyle (x_{0},f(x_{0}))}$ geht und die Steigung ${\displaystyle g}$ besitzt:

${\displaystyle G=\{(x,y)\in \mathbb {R} ^{2}\mid y=g\cdot (x-x_{0})+f(x_{0})\}}$

Da die Normalengleichung von ${\displaystyle G}$ gerade

${\displaystyle -g\cdot (x-x_{0})+1\cdot (y-f(x_{0}))=0}$

ist, ist die Normale an ${\displaystyle G}$ also ${\displaystyle (-g,1)\in \mathbb {R} ^{2}}$

Im allgemeinen Fall ${\displaystyle n\geq 1}$ liegt ${\displaystyle f}$ über der Hyperebenen, die durch den Fußpunkt ${\displaystyle (x_{0},f(x_{0}))}$ und die Normale ${\displaystyle (-g,1)\in \mathbb {R} ^{n+1}}$ gegeben ist.

Wegen d​es Trennungssatzes i​st das Subdifferential e​iner stetigen konvexen Funktion überall n​icht leer.

Beispiel

Das Subdifferential der Funktion ${\displaystyle f\colon \mathbb {R} \rightarrow \mathbb {R} }$, ${\displaystyle x\mapsto |x|}$ ist gegeben durch:

${\displaystyle \partial f(x_{0})={\begin{cases}\{-1\}&x_{0}<0\\\left[-1,1\right]&x_{0}=0\\\{1\}&x_{0}>0\end{cases}}}$

Beschränktheit

Sei ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$ stetig und sei ${\displaystyle X\subset \mathbb {R} ^{n}}$ beschränkt. Dann ist die Menge ${\displaystyle \bigcup _{x_{0}\in X}\partial f(x_{0})}$ beschränkt.

Beweis

Sei ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$ stetig und sei ${\displaystyle X\subset \mathbb {R} ^{n}}$ beschränkt. Setze ${\displaystyle \varepsilon$ :=\sup |f({\overline {U_{1}(X)}})|} wobei ${\displaystyle {\overline {U_{1}(X)}}=\{x\in \mathbb {R} ^{n}\mid {\rm {dist}}(x,X)\leq 1\}}$. Angenommen ${\displaystyle \bigcup _{x_{0}\in X}\partial f(x_{0})}$ ist nicht beschränkt, dann gibt es für ${\displaystyle R:=2\varepsilon }$ ein ${\displaystyle x_{0}\in X}$ und ein ${\displaystyle g\in \partial f(x_{0})}$ mit ${\displaystyle \|g\|_{2}>R=2\varepsilon }$. Sei ${\displaystyle x:={\frac {1}{\|g\|_{2}}}g+x_{0}}$. Somit sind ${\displaystyle x_{0},x\in {\overline {U_{1}(X)}}}$. Wir erhalten die Abschätzung

${\displaystyle g^{T}(x-x_{0})={\frac {1}{\|g\|_{2}}}g^{T}g=\|g\|_{2}>2\varepsilon \geq \left|f(x)-f(x_{0})\right|\geq f(x)-f(x_{0})}$.

${\displaystyle g}$ ist also kein Subgradient. Das ist ein Widerspruch.

Differenzierbarkeit

Ist die Funktion differenzierbar in ${\displaystyle x_{0}\in \mathrm {int} \,\mathrm {dom} \,f}$, so gilt:

${\displaystyle \partial f(x_{0})=\left\{\nabla f(x_{0})\right\}}$

Siehe [3] für e​inen Beweis.

Zudem gilt: Ist das Subdifferential ${\displaystyle \partial f(x_{0})}$ einelementig, so ist ${\displaystyle f}$ an der Stelle ${\displaystyle x_{0}}$ differenzierbar[4]

Literatur

1. R. T. Rockafellar Convex analysis 1970., p.214
2. R. T. Rockafellar Convex analysis 1970., p.215
3. Prof. Yaron Singer: Advanced Optimzation. Abgerufen am 27. Januar 2022: „Proposition 4“
4. R.T. Rockafellar: Convex Analysis. Band 28, 1970: „Theorem 25.1“