Spiegelladung

Die Spiegelladung oder Bildladung ist eine gedankliche Hilfsstütze, um das Verhalten einer Ladung Q vor einem leitenden Körper oder einer dielektrischen Grenzfläche im Abstand R zu veranschaulichen. Beim Fall eines Leiters wird die gesamte influenzierte Ladung dafür anschaulich zu einer Punktladung zusammengefasst. Aus Symmetriegründen wird diese Punktladung als Spiegelladung bezeichnet. Sie ist damit ein Spezialfall des Ladungsschwerpunktes einer influenzierten Ladung.

Spiegelladung einer positiven Ladung an einer Metallfläche

Das dazugehörige Prinzip der Spiegelladung ist eine Methode zur Lösung elektrostatischer Randwertprobleme.

Grundlagen

Wird ein leitender Körper in ein äußeres elektrisches Feld gebracht, so stehen meistens zu Beginn die Feldlinien noch nicht senkrecht auf der Oberfläche. Dies führt zu Potentialunterschieden entlang der Oberfläche, welche die frei beweglichen Elektronen dazu bringen sich so zu verschieben, dass die Feldlinien senkrecht auf die Oberfläche treffen (äußere elektrische Felder nehmen innerhalb leitender Körper exponentiell mit der Zeit ab). Da das äußere elektrische Feld auch Potentialunterschiede im Körper verursacht, bewegen sich die Elektronen innerhalb des Körpers so, dass dort überall das gleiche Potential herrscht. Theoretisch führt das demzufolge zu Oberflächenladungsdichten. Mikroskopisch nah betrachtet halten die Elektronen zueinander einen Abstand und deshalb befinden sich die Influenzladungen immer nur sehr nahe an der Oberfläche, sind aber keine echten Oberflächenladungen.

Da die elektrischen Feldlinien senkrecht auf der Oberfläche stehen, verändert der leitende Körper das elektrische Feld so, dass seine Oberfläche mit einer Äquipotentialfläche übereinstimmt. Zur mathematischen Behandlung wird demzufolge zu dem vorhandenen äußeren elektrischen Feld ein zweites elektrisches Feld eingeführt mit der Randbedingung, dass das superponierte Feld senkrecht auf der Oberfläche steht. Dies ist gleichbedeutend mit der Forderung, dass das elektrische Potential an der Oberfläche überall konstant, der Einfachheit halber gleich 0 ist.

Die Umkehrung dieser Vorgehensweise ist, dass man bei einem gegebenen elektrischen Feld entlang der Äquipotentialflächen das Feld abschneidet und dort leitende Oberflächen platziert (natürlich unter Erhaltung der Form der Äquipotentialfläche). Diese Vorgehensweise ist mit Mitteln der Funktionentheorie ein sehr mächtiges Werkzeug zur Lösung bestimmter Randwertaufgaben.

Anwendungsbeispiele

Metallplatte

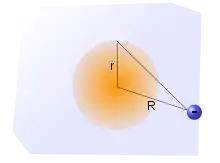
Punktladung vor einer ungeladenen Metallplatte

Durch Influenz wird von der Ladung Q in der Metallplatte eine entgegengesetzte Ladung erzeugt. Die elektrischen Feldlinien sowie die Coulombkräfte zwischen erzeugender Ladung und Platte verhalten sich so, als ob sich eine Ladung -Q im Abstand R hinter der Metallplatte befindet. Die erzeugende Ladung wird also – bildhaft gesprochen – an der Metalloberfläche gespiegelt.

Für die Anordnung der influenzierten Ladungen werden Oberflächenladungen auf der Metalloberfläche angenommen. Die Ladungsdichte auf der Oberfläche hat an der Stelle, über der die Ladung Q senkrecht steht ihr Maximum und fällt radial nach außen ab. Geht man von einer unendlich ausgedehnten, elektrisch perfekt leitenden Metallplatte aus, so lässt sich die Oberflächenladungsdichte wie folgt als Formel angeben[1]:

\sigma (r)=-{\frac {Q\cdot R}{2\pi \cdot \left(r^{2}+R^{2}\right)^{\frac {3}{2}}}}

Andere leitende Objekte

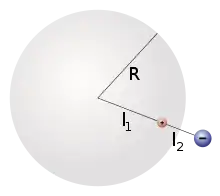
Punktladung vor einer ungeladenen Metallkugel

Bei anderen leitenden Objekten, wie beispielsweise einer Metallkugel, liegt die Spiegelfläche nicht zwangsweise auf der Oberfläche. Es lässt sich jedoch in den meisten Fällen eine einzelne, gedankliche Punktladung konstruieren, in welcher man sich die gesamte Ladung vereint vorstellen kann (Ladungsschwerpunkt). Bei der Analyse ist zu beachten, ob die Kugel geerdet oder nicht geerdet ist[2].

Im Falle einer unendlich gut leitenden Kugel mit Radius R lässt sich die Spiegelladung über die Inversion am Kreis (gedanklich Spiegelung an der Kreisoberfläche) finden. Für die Abstände der Spiegelladung gilt (geerdet oder ungeerdet) dann:

l_{1}={\frac {R^{2}}{l_{1}+l_{2}}}={\frac {R^{2}}{L}}

Für den Betrag der gespiegelten Ladung $q'$ gilt dann:

q'=q\cdot {\frac {R}{L}}

Planare dielektrische Grenzfläche

Gegeben sei eine planare dielektrische Grenzfläche. In dem Medium mit Dielektrizitätszahl $\epsilon _{1}$ befinde sich eine Ladung $q$ am Ort ${\vec {s}}$ . In dem anderen Medium stellt man sich dann die Ladung $q'={\frac {\epsilon _{1}-\epsilon _{2}}{\epsilon _{1}+\epsilon _{2}}}q$ vor. Für den Fall $\epsilon _{1}>\epsilon _{2}$ ist ${\text{sign}}(q')={\text{sign}}(q)$ und in beiden Medien liegen somit gleichnamige Ladungen vor, die sich abstoßen. Für den Fall $\epsilon _{1}<\epsilon _{2}$ ist ${\text{sign}}(q')\neq {\text{sign}}(q)$ und die ungleichnamigen Ladungen ziehen sich an. Daher werden Ladungen, die sich in einem Dielektrikum befinden von dielektrischen Grenzflächen abgestoßen, falls das andere Dielektrikum eine kleinere Dielektrizitätszahl hat. Dieses Verhalten lässt sich auch durch eine Energiebetrachtung verstehen.

Literatur

Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik. 18. Auflage. Springer, 2008, ISBN 978-3-540-78589-7, Kapitel 10 - Einfache Beispiele für elektrostatische Felder.

Weblinks

Animation zur Spiegelladung an einer Metallfläche

Einzelnachweise

Walter Greiner: Klassische Elektrodynamik. 6. überarbeitete Auflage. Wissenschaftlicher Verlag Harri Deutsch GmbH, Frankfurt am Main 2002, ISBN 3-8171-1660-8, S. 53 f.
Walter Greiner: Klassische Elektrodynamik. 6. überarbeitete Auflage. Wissenschaftlicher Verlag Harri Deutsch, Frankfurt am Main 2002, ISBN 3-8171-1660-8, S. 45 ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Walter Greiner: Klassische Elektrodynamik. 6. überarbeitete Auflage. Wissenschaftlicher Verlag Harri Deutsch GmbH, Frankfurt am Main 2002, ISBN 3-8171-1660-8, S. 53 f.

[2] Walter Greiner: Klassische Elektrodynamik. 6. überarbeitete Auflage. Wissenschaftlicher Verlag Harri Deutsch, Frankfurt am Main 2002, ISBN 3-8171-1660-8, S. 45 ff.