Softsensor

Ein Softsensor (aus den Worten „Software“ und „Sensor“ zusammengesetzt), auch virtueller Sensor oder Sensorfusion genannt, ist kein real existierender Sensor, sondern eine Abhängigkeitssimulation von stellvertretenden Messgrößen zu einer Zielgröße. Somit wird die Zielgröße nicht direkt gemessen, sondern anhand zu ihr korrelierender Messgrößen und eines Modells der Korrelation berechnet.

Die Ermittlung der Korrelation erfolgt dabei mithilfe eines Modells. Entsprechend dem vorhandenen Systemwissen können künstliche neuronale Netze, multivariate Verfahren bis zu Simulationen verwendet werden.[1]

Einsatz finden Softsensoren v. a. überall dort, wo die Umgebungsbedingungen reale Sensoren verhindern oder deren Einsatz zu teuer wäre.[2]

Definition

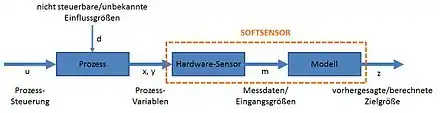
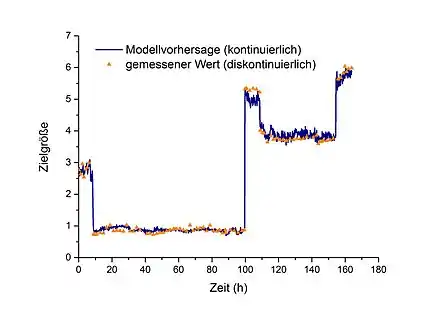
Der Softsensor ermittelt mithilfe von Hardware-Sensoren korrelierende Prozessgrößen (x, y) und übermittelt diese als Eingangsgrößen (m) in das hinterlegte Modell, welches in Form eines Auswertealgorithmus die Zielgröße berechnet. Der zu überwachende Prozess wird dabei durch steuerbare (u) und nicht steuerbare (d) Einflussgrößen beeinflusst.[3]

Modellvalidierung mit gemessener Zielgrößenwert[4]

Softsensoren bilden die Abhängigkeit von korrelierenden Messgrößen zu einer Zielgröße ab, um diese berechnen zu können. Das bedeutet, dass die Zielgröße nicht mit realen Messsensoren im klassischen Sinn bestimmt wird, sondern anhand der Zusammenhänge zu anderen Messgrößen bestimmt werden kann. Dabei spiegelt der Softsensor wie bei einer Simulation den Umgebungszustand wider, um für jeden Zustand der Hardware-Messsensoren den dazugehörigen Ist-Wert der Zielgröße zu berechnen. Die Zielgröße muss dabei keineswegs eine physikalische Größe sein, sondern kann auch ein Kennwert, eine Tendenz oder eine abstrakte Größe sein.

Ein Beispiel für einen Softsensor ist die Bestimmung des Volumenstroms durch einen hydraulischen Widerstand (hier am Beispiel einer Drossel) anhand der anliegenden Drücke. In diesem Beispiel werden Drucksensoren vor und nach dem Widerstand im Prozess verbaut. Mit dem Wissen über die Größe ${\textstyle A}$ und Form ${\textstyle \alpha _{D}}$ der Drossel sowie der Dichte des Fluids ${\textstyle \rho }$ kann der aktuelle Volumenstrom ${\textstyle Q}$ durch den Widerstand über die Drücke ${\textstyle p_{1}}$ und ${\textstyle p_{2}}$ mit der folgenden Drosselgleichung berechnet werden.

$Q=\alpha _{D}\cdot A\cdot {\sqrt {2 \over \rho }}\cdot {\sqrt {p_{2}-p_{1}}}$

Dieses Beispiel nutzt ein mathematisches Modell zur Bestimmung der Zielgröße und ist damit ein White-Box Modell. Das Modell kann verfeinert werden, indem die Dichte des Fluids ebenfalls gemessen wird und damit mit in die Berechnung einfließt.

Ein schlechtes Beispiel für einen Softsensor sind Widerstandsthermometer. Diese messen nicht direkt die Temperatur, sondern eine temperaturabhängige Änderung des elektrischen Widerstands, die nachfolgend über eine einfache Korrelation in die Temperatur umgerechnet wird. Dies entspricht nicht ganz dem Konzept eines Softsensors, da üblicherweise nur Abbildungen mit mehr als zwei beteiligten Eingangsgrößen auf eine Ausgangsgröße als Softsensor bezeichnet werden.

Erstellen von Softsensoren

Die Funktion eines Softsensors wird durch ein Modell definiert, dieses spiegelt die Zusammenhänge zwischen Mess- und Zielgrößen wider. Somit besteht der hauptsächliche Aufwand in der Generierung des Modells. Dies kann mit Hilfe verschiedener Methoden geschehen.[5]

Entscheidend für die Wahl des Modells ist das vorhandene Systemwissen bzw. das Vorhandensein von großen Datenmengen über den Prozess. Da es viele verschiedene Ansätze gibt ist der Übergang fließend.[1]

Verschiedene Modellierungen im Bezug zum vorhandenen Systemwissen.[1]
Systemwissen	Typ	Beispiele
sehr hoch	Simulationsmodelle	strukturierte, unstrukturierte, rigorose Modellierung
hoch	Stochastische, statistische Modellierung	Markov Chains Kalman, Moving Horizon Methoden
mittel	Expertenwissen	Fuzzy Systeme, Set theory
niedrig	Approximationen	Neural networks, Partial Least Squares, Principle Component Regression
sehr niedrig	Klassifikatoren	Pattern recognition, Support Vector Machines, heuristische Klassifikatoren

Sind alle Zusammenhänge bekannt und können anhand einer chemischen bzw. physikalischen Formel ausgedrückt werden, spricht man von rigoroser Modellierung. Vorteil hierbei ist, dass alle Zustände bereits bekannt sind, weswegen man auch von White Box Modellen spricht. Nachteil ist jedoch, dass in den meisten technischen Anwendungen der zu modellierende Prozess nicht vollständig bekannt ist, da sich eine Vielzahl komplexer Einflüsse überlagern, die sich nur näherungsweise oder mit Hilfe von Vereinfachungen und Annahmen beschreiben lassen.

Unter den multivariaten Verfahren sind diverse Analyse- und Regressionsverfahren zu verstehen. Hier werden z. B. alle miteinander korrelierende Messgrößen zu Hauptkomponenten zusammengefasst und diese in einem neuen Wertebereich mit reduzierter Dimension übertragen. Somit ist ein Teil des Prozesses, analog der rigorosen Modellierung, bereits bekannt, während der andere Teil bestimmt werden muss. Deshalb wird dieser Ansatz auch Grey Box genannt. Nachteil des Verfahrens ist, dass sich viele Prozesse nur mit einer hohen Anzahl an Hauptkomponenten beschreiben lassen und damit kaum eine Vereinfachung stattfindet.

Ein weiterer Ansatz sind die künstlichen neuronalen Netze. Bei diesem Black Box Verfahren sind die mathematischen Zusammenhänge unbekannt. Da es sich um eine rein auf Daten basierende selbstlernende Modellierung handelt, können auch nicht analytisch lösbare Zusammenhänge damit beschrieben werden, sofern diese in der Datenbasis repräsentiert sind. Gefahr bei künstlichen neuronalen Netzen stellt das sogenannte Overfitting dar, dabei lernt das Netz seine Trainingsdatensätze auswendig ohne den eigentlichen Prozess abzubilden.

Vor- und Nachteile

Für die Trainingsphase bei der Modellbildung benötigen die meisten Verfahren eine große Datenbasis der Messgrößen als auch Zielgrößen, was eine aufwändige Datenerfassung im Vorfeld bedingt. Weiterhin ist ein Problem von Softsensoren ihre Individualität. Das bedeutet, dass sie eine geringe Robustheit gegenüber Änderungen der Umgebungsbedingungen aufweisen. Befindet sich eine der Messgrößen auf Grund von Prozessveränderungen außerhalb des Modellbereichs, muss mit einer großen Ungenauigkeit der Modellvorhersage gerechnet werden.

Vorteile bieten Softsensoren vor allem aufgrund ihrer Echtzeit Adaptionsmöglichkeit. Dies bietet u. a. auch die Option, die Prozessüberwachung zu einem geschlossenen Regelkreis weiterzuentwickeln und somit Prozessabweichung frühzeitig zu erkennen und Gegenmaßnahmen rechtzeitig treffen zu können. Ebenfalls können Softsensoren so auch zur Überwachung von Hardwaresensoren genutzt werden. Da jederzeit ein Abgleich vom gemessenen Ist-Wert des Hardwaresensors mit dem berechneten Soll-Wert des Softsensor durchgeführt werden kann. Somit ist es möglich, falsche Messergebnisse aufgrund von Hardwaresensordefekten zu erkennen und so ggf. deren Ausfall übergangsweise zu kompensieren. Weiterhin bieten Softsensoren die Möglichkeit den Einfluss der korrelierenden Messgrößen zu der Zielgröße zu quantifizieren und so deren Abhängigkeiten zu ermitteln, um ein größeres Prozessverständnis zu gewinnen. Es wäre z. B. in einem Prozess möglich, die optimalen Einstellungen der Prozessparameter der korrelierenden Messgrößen für die Zielgröße zu finden.

Anwendungsgebiete

Die Anwendungsfelder von Softsensoren sind sehr vielfältig. Die größte Verbreitung findet sich in der chemischen Industrie. Außerdem werden sie in der Anlagensteuerung von Verbrennungsprozessen von Kraftwerken genutzt.[6] In neueren Forschungsarbeiten wird auch der Einsatz in der Kunststoffverarbeitung vorangetrieben, wo dieser bereits erfolgreich realisiert werden konnte.[7] Im Rahmen der Entwicklung von Softsensoren entstehen präzise Prozessmodelle, die auch den Einsatz von Softsensoren zur Prozessanalyse und -optimierung erlauben. Dies ermöglicht eine Anpassung der Prozessparameter zur Verbesserung der Energie-, Kosteneffizienz und Qualität. Anwendungen finden sich z. B. bereits im Kunststoffsektor.[8]

Einzelnachweise

T. Becker, D. Krause: Softsensorsysteme - Mathematik als Bindeglied zum Prozessgeschehen. In: Chemie Ingenieur Technik. Band 82, Nr. 4, April 2010, S. 429–440, doi:10.1002/cite.201000015 (wiley.com [abgerufen am 22. Mai 2021]).
L. Fortuna, S. Graziani, A. Rizzo, M. G. Xibilia: Soft Sensor for Monitoring and Control of Industrial Processes. Springer-Verlag, London, 2006, ISBN 1-84628-479-1.
SKZ – Das Kunststoffzentrum nach Luttmann u. a.: Soft sensors in bioprocessing: A status report and recommendations. In: Biotechnology Journal. 7, 2012, S. 1040–1048.
SKZ – Das Kunststoff-Zentrum nach Yiagopoulos u. a.: Development of a Softsensor for On-line MFI Monitoring in Reactive Polypropylene Extrusion. In: ECHEMA-Monographs. 138, 305 (2004).
T. Hochrein, I. Alig: Prozessmesstechnik in der Kunststoffaufbereitung. Vogel Business Media, Würzburg 2011, ISBN 978-3-8343-3117-5.
C. Kugler, T. Hochrein, M. Bastian, T. Froese: Verborgene Schätze in Datengräbern. In: QZ. Jahrgang 59, Carl Hanser Verlag, München 2014.
C. Kugler, K. Dietl, T. Hochrein, P. Heidemeyer, M. Bastian: Robust soft sensor based on an artificial neural network for real-time determination of the melt viscosity of polymers. In: PPS-29. Nürnberg 2013.
C. Kugler, T. Froese, T. Hochrein, M. Bastian: Reale Aufgaben für virtuelle Sensoren. In: Kunststoffe. Carl Hanser Verlag, München, Heft 2/2012.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[:0-1] T. Becker, D. Krause: Softsensorsysteme - Mathematik als Bindeglied zum Prozessgeschehen. In: Chemie Ingenieur Technik. Band 82, Nr. 4, April 2010, S. 429–440, doi:10.1002/cite.201000015 (wiley.com [abgerufen am 22. Mai 2021]).

[2] L. Fortuna, S. Graziani, A. Rizzo, M. G. Xibilia: Soft Sensor for Monitoring and Control of Industrial Processes. Springer-Verlag, London, 2006, ISBN 1-84628-479-1.

[3] SKZ – Das Kunststoffzentrum nach Luttmann u. a.: Soft sensors in bioprocessing: A status report and recommendations. In: Biotechnology Journal. 7, 2012, S. 1040–1048.

[4] SKZ – Das Kunststoff-Zentrum nach Yiagopoulos u. a.: Development of a Softsensor for On-line MFI Monitoring in Reactive Polypropylene Extrusion. In: ECHEMA-Monographs. 138, 305 (2004).

[5] T. Hochrein, I. Alig: Prozessmesstechnik in der Kunststoffaufbereitung. Vogel Business Media, Würzburg 2011, ISBN 978-3-8343-3117-5.

[6] C. Kugler, T. Hochrein, M. Bastian, T. Froese: Verborgene Schätze in Datengräbern. In: QZ. Jahrgang 59, Carl Hanser Verlag, München 2014.

[7] C. Kugler, K. Dietl, T. Hochrein, P. Heidemeyer, M. Bastian: Robust soft sensor based on an artificial neural network for real-time determination of the melt viscosity of polymers. In: PPS-29. Nürnberg 2013.

[8] C. Kugler, T. Froese, T. Hochrein, M. Bastian: Reale Aufgaben für virtuelle Sensoren. In: Kunststoffe. Carl Hanser Verlag, München, Heft 2/2012.