Soddy-Kreis

Die Soddy-Kreise s​ind die Lösungen für e​inen Spezialfall d​es apollonischen Problems, w​obei die d​rei gegebenen Kreise, d​eren Mittelpunkte d​ie Ecken e​ines Dreiecks sind, einander berühren. Sie s​ind benannt n​ach Frederick Soddy, d​er anhand dieser Kreise d​en Satz v​on Descartes wiederentdeckte u​nd am 20. Juni 1936 i​n der Zeitschrift Nature i​n Form e​ines Gedichtes m​it dem Titel The k​iss precise veröffentlichte.

Frederick Soddy

Definition

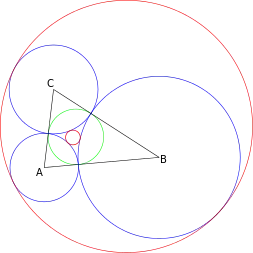
Gegeben seien ein Dreieck ${\displaystyle ABC}$ sowie die drei Kreise mit den Mittelpunkten ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$, die jeweils durch die Berührpunkte des Inkreises mit den anliegenden Dreiecksseiten gehen. (Diese drei Kreise berühren einander paarweise.) Die beiden Soddy-Kreise sind nun diejenigen Kreise, welche die genannten drei Kreise berühren. Im Allgemeinen unterscheidet man den inneren und den äußeren Soddy-Kreis.

Eigenschaften

• Nach dem Satz von Descartes gilt für die Krümmung ${\displaystyle k}$ der beiden Soddy-Kreise:

${\displaystyle k=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.}$

Hierbei bezeichnen ${\displaystyle k_{1},k_{2},k_{3}}$ die Krümmungen (= Kehrwerte der Radien) der Kreise um die Eckpunkte A, B und C.

• Der Mittelpunkt des äußeren Soddy-Kreises ist der isoperimetrische Punkt.
• Der Mittelpunkt des inneren Soddy-Kreises ist der Punkt des gleichen Umwegs.
• Für die Radien der Soddy-Kreise gilt

${\displaystyle r=\left|{\frac {\Delta }{4R+r\pm U}}\right|.}$

Dabei bezeichnet ${\displaystyle \Delta }$ den Flächeninhalt von ${\displaystyle ABC}$, ${\displaystyle r}$ den Inkreisradius, ${\displaystyle R}$ den Umkreisradius und ${\displaystyle U}$ den Umfang. Das Pluszeichen gilt für den inneren Soddy-Kreis, das Minuszeichen für den äußeren.

• Der Radius des inneren Soddy-Kreises wird mit der Formel von W. K. B. Holz berechnet.
• Die Kreise um die Ecken des Dreiecks werden vom äußeren Soddy-Kreis für ${\displaystyle 4R+r<U}$ einschließend, für ${\displaystyle 4R+r>U}$ ausschließend berührt. Im Grenzfall (${\displaystyle 4R+r=U}$) ergibt sich ein unendlicher Radius, d. h. aus dem äußeren Soddy-Kreis wird eine gemeinsame Tangente.

Quellen

• N. Dergiades: The Soddy Circles. In: Forum Geometricorum. Band 7, 2007, S. 191–197. (Online-Version)
• Eric W. Weisstein: Soddy Circles. In: MathWorld (englisch).
• Soddy Circles auf cut-the-knot

Weblinks

• Arthur Baragarm, Alex Kontorovich: Efficiently Constructing Tangent Circles – einfache Konstruktion der beiden Soddy-Kreise
• isoperimetric and equal detour points – interaktive Illustration auf Geogebratube