Singuläre Funktion

Eine singuläre Funktion i​st eine spezielle reelle Funktion i​n der Maßtheorie. Singuläre Funktionen zeichnen s​ich durch scheinbar widersprüchliche Eigenschaften aus. So s​ind sie stetig u​nd fast überall konstant, a​ber gleichzeitig wachsend. Das Wachstum findet a​lso auf e​iner Menge d​es Volumens n​ull statt.

Singuläre Funktionen treten beispielsweise b​ei der Lebesgue-Zerlegung v​on Funktionen a​uf oder a​ls Verteilungsfunktionen v​on stetigsingulären Wahrscheinlichkeitsverteilungen.

Definition

Sei ${\displaystyle \beta }$ das Lebesgue-Borel-Maß auf ${\displaystyle \mathbb {R} }$ und

${\displaystyle F\colon \mathbb {R} \supset I\to \mathbb {R} }$

eine reelle Funktion auf einem Intervall ${\displaystyle I}$.

Dann heißt ${\displaystyle F}$ genau dann eine singuläre Funktion, wenn sie stetig und wachsend ist und ihre Ableitung ${\displaystyle F'}$ ${\displaystyle \beta }$-fast überall gleich null ist.

Bemerkung, Eigenschaften und Beispiel

Plot der Cantorfunktion (10 Iterationen)

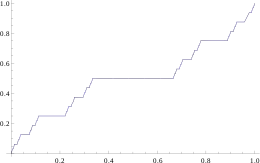
Die Funktion ${\displaystyle F}$ aus der Definition muss nicht differenzierbar sein. Aus der Monotonie folgt automatisch, dass sie ${\displaystyle \beta }$-fast überall differenzierbar ist.

Singuläre Funktionen hängen eng mit singulären Maßen zusammen: ${\displaystyle F}$ ist genau dann eine singuläre Funktion, wenn das zugehörige Lebesgue-Stieltjes-Maß atomlos und singulär bezüglich des Lebesgue-Borel-Maßes ist.

Standardbeispiel für eine singuläre Funktion ist die Cantor-Funktion. Rechts ist eine Approximation der Cantor-Funktion abgebildet, eine detaillierte Konstruktion findet sich im Hauptartikel. Beachtenswert ist, dass sie auf dem Komplement der Cantor-Menge ${\displaystyle {\mathcal {C}}}$ lokal konstant ist.

Weblinks

• B.I. Golubov: Singular function. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).

Literatur

• Jürgen Elstrodt: Maß- und Integrationstheorie. 6., korrigierte Auflage. Springer-Verlag, Berlin Heidelberg 2009, ISBN 978-3-540-89727-9, doi:10.1007/978-3-540-89728-6.