Silver-Meal Heuristik

Die Silver-Meal Heuristik ist ein heuristisches Verfahren der Dynamischen Losgrößenermittlung. Damit werden für die Produktion Losgrößen ermittelt, welche die Bedarfe abdecken und gleichzeitig die Gesamtkosten minimieren. Das Verfahren wurde 1973 von Edward A. Silver und Harlan C. Meal veröffentlicht.

Voraussetzung und Fragestellung

Für zukünftige Perioden (Wochen, Monate …) seien die Bedarfe oder die Nachfragen eines Produktes bekannt. Um ein Los zu produzieren, fallen Rüstkosten K [Euro/Los] an, die Lagerhaltungskosten betragen h [Euro/Stück/Periode].

Gesucht ist ein Produktionsplan, bei dem die Gesamtkosten möglichst gering ausfallen.

Zielkonflikt

Kostenverlauf bei Losfertigung

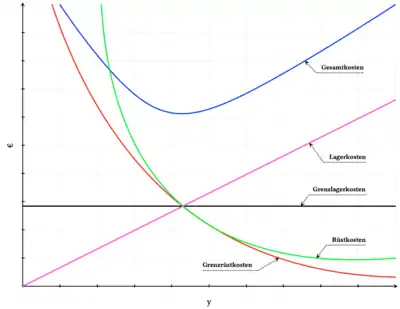
Fertigt man mit weniger und dafür größeren Losen, dann reduzieren sich die Rüstkosten, dafür erhöhen sich die Lagerhaltungskosten. Umgekehrt führen mehr Lose zu niedrigeren Lagerkosten, dafür aber zu höheren Rüstkosten.

Silver-Meal-Heuristik

Die Silver-Meal-Heuristik betrachtet zunächst ein Los, welches den Bedarf für eine Periode abdeckt, und ermittelt die Kosten. Danach erhöht es die Losgröße derart, dass der Bedarf für eine weitere Periode abgedeckt wird und berechnet die durchschnittlichen Kosten für diese Perioden. Es wird solange jeweils eine Periode hinzugenommen, bis sich die durchschnittlichen Kosten pro Periode erhöhen. Hier bricht das Verfahren ab.

Produziert man für die Bedarfe der Perioden t bis t+n, dann errechnen sich die durchschnittlichen Kosten aus

$Z(t,t+n)={\frac {1}{n+1}}\left(K+h\sum _{k=0}^{n}{k\cdot y_{t+k}}\right)$

n = Anzahl der Perioden

K = Rüstkosten für ein Los [Euro/Los]

h = Lagerhaltungskosten in Euro pro Stück und Periode [Euro/Stück/Periode]

y_{t+k}

= Produktionsmenge in der Periode t+k

Das Verfahren bricht ab, wenn Z (t,t+n) < Z (t,t+(n+1)) = Z (t,t+n+1).

Durch elementare Umformungen lässt sich die Abbruchsbedingung auch schreiben als

Z(t,t+n)<h\cdot (n+1)\cdot y_{t+n+1}

Beispiel[1]

Für die Perioden 8 bis 12 fallen folgende Bedarfe in Stück an: 27, 22, 13, 19, 12. Die Rüstkosten betragen K = 200 Euro, die Lagerkosten 10 Euro/Stück/Periode.

Produziert man am Anfang von Periode 8 nur für Periode 8, also ein Los mit 27 Stück, dann fallen nur Rüstkosten, aber keine Lagerkosten an. Die Kosten betragen daher Z (8,8) = 200 Euro.

Produziert man am Anfang von Periode 8 für die Perioden 8 und 9, also ein Los mit 49 Stück, dann entstehen 200 Euro Rüstkosten. Zudem müssen 22 Stück für die Folgeperiode eingelagert werden, was zu Lagerkosten von 22*10 Euro = 220 Euro führt. Die durchschnittlichen Kosten für die Perioden 8 und 9 sind daher Z (8,9) = (200 Euro + 220 Euro)/2 = 210 Euro.

Da Z (8,8) < Z (8,9) ist, sich die durchschnittlichen Kosten also bei zwei Perioden erhöhen, bildet man ein Los, das nur den Bedarf für Periode 8 abdeckt.

Analog müssen nun die verbleibenden Perioden 9 bis 12 untersucht werden:

Z (9,9) = 200 Euro

Z (9,10) = (200 Euro + 13*10 Euro)/2 = 165 Euro < Z (9,9)

Z (9,11) = (200 Euro + 13*10 Euro + 2*19*10 Euro)/3 = 710/3 Euro = 236,66 Euro > Z (9,10) 19 Stück werden zwei Perioden lang gelagert

Somit wird am Anfang von Periode 9 für die Perioden 9 und 10 produziert mit einer Losgröße von 35 Stück.

Für die verbleibenden Perioden 11 bis 12 ergibt sich.

Z (11,11) = 200 Euro

Z (11,12) = (200 Euro + 12*10 Euro)/2 = 160 Euro < Z (11,11)

Produktionsmengen und Bestände
Periode t	8	9	10	11	12	Summe Kosten
Anfangsbestand l_t	0	0	13	0	12
Bedarf y_t	27	22	13	19	12
Losgröße x_t	27	35	0	31	0
Endbestand l_t+1	0	13	0	12	0
Rüstkosten	200	200	0	200	0	600
Lagerkosten	0	130	0	120	0	250

Es werden drei Lose aufgelegt. Eingelagert werden 13 und 12 Stück für jeweils eine Periode. Die Gesamtkosten betragen

Z = Rüstkosten + Lagerkosten = 3*200 Euro + (13 Stück + 12 Stück)*10 Euro/Stück = 850 Euro.

Lösung nicht immer optimal

Die Lösungen der Silver-Meal-Heuristik sind nicht immer optimal. Das liegt daran, dass das Verfahren abbricht, sobald die durchschnittlichen Kosten steigen. Diese durchschnittlichen Kosten könnten jedoch auch wieder fallen, wenn man weitere Perioden für die Losbildung hinzunimmt.

Das folgende Beispiel zeigt eine nicht-optimale Lösung.[2]

Produktionsmengen und Bestände nach Silver-Meal
Periode t	20	21	22	23	Summe Kosten
Anfangsbestand l_t	0	1	0	1
Bedarf y_t	3	1	7	1
Losgröße x_t	4	0	8	0
Endbestand l_t+1	1	0	1	0
Rüstkosten	200	0	200	0	400
Lagerkosten	10	0	10	0	20

Hier werden zwei Lose aufgelegt, die Kosten betragen

Z={\text{Rüstkosten}}+{\text{Lagerkosten}}=2\cdot 200{\text{ Euro}}+(1{\text{ Stück}}+1{\text{ Stück}})\cdot 10{\frac {\text{Euro}}{\text{Stück}}}=420{\text{Euro}}

.

Würde man dagegen den gesamten Bedarf mit einem einzigen Los in Periode 20 produzieren, dann ergäbe sich folgende Lösung:

Besseres Produktionsprogramm
Periode t	20	21	22	23	Summe Kosten
Anfangsbestand l_t	0	9	8	1
Bedarf y_t	3	1	7	1
Losgröße x_t	12	0	0	0
Endbestand l_t+1	9	8	1	0
Rüstkosten	200	0	0	0	200
Lagerkosten	90	80	10	0	180

Hier betragen die Kosten nur

Z = Rüstkosten + Lagerkosten = 1*200 Euro + (9 Stück + 8 Stück + 1 Stück)*10 Euro/Stück = 380 Euro.

Kritik am Silver-Meal Verfahren

Das Silver-Meal Verfahren berücksichtigt keine Kapazitäten. Dies kann zu nicht realisierbaren Lösungen führen, weil etwa der benötigte Lagerraum nicht zur Verfügung steht oder die errechneten Losgrößen wegen fehlender Kapazitäten nicht gefertigt werden können. Auch werden die Lagereigenschaften des Produkts, etwa dessen Haltbarkeit, vernachlässigt.

Siehe auch

Literatur

Edward A. Silver, Harlan C. Meal (1973): A heuristic for selecting lot size requirements for the case of a deterministic time-varying demand rate and discrete-opportunities for replenishment. Production and Inventory Management 14(2), 64–74.
Christian Ortmann, Ingo Siebeking: Heuristiken zur Losgrößenplanung in PPS-Systemen, Prämierte Diplomarbeit im Fachbereich Wirtschaftswissenschaften der Universität Osnabrück, Juni 2000 Online (Memento vom 26. November 2013 im Internet Archive) (abgerufen am 7. Februar 2016)

Einzelnachweise

Das Beispiel ist entnommen aus dem Vorlesungsskript von Prof. Dr. Ulrich Thonemann zum Thema "Operations Management - Produktionsplanung" im Wintersemester 2011/2012 an der Universität Köln
Prof. Dr. Ulrich Thonemann: Operations Management: Konzepte, Methoden und Anwendungen, Verlag: Pearson Studium; Auflage: 2., aktualisierte und erweiterte Auflage. (8. April 2010), ISBN 978-3827373168, Seite 314–315 Online (abgerufen am 24. Dezember 2011)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Thonemann-Vorlesung-1] Das Beispiel ist entnommen aus dem Vorlesungsskript von Prof. Dr. Ulrich Thonemann zum Thema "Operations Management - Produktionsplanung" im Wintersemester 2011/2012 an der Universität Köln

[Thonemann-G-books-2] Prof. Dr. Ulrich Thonemann: Operations Management: Konzepte, Methoden und Anwendungen, Verlag: Pearson Studium; Auflage: 2., aktualisierte und erweiterte Auflage. (8. April 2010), ISBN 978-3827373168, Seite 314–315 Online (abgerufen am 24. Dezember 2011)