Sharadchandra Shankar Shrikhande

Sharadchandra Shankar Shrikhande (häufig als S. S. Shrikhande zitiert; * 19. Oktober 1917 in Sagar, Central Provinces [heute Madhya Pradesh]; † 21. April 2020 in Vijayawada, Andhra Pradesh[1]) war ein indischer Mathematiker.

Shrikhande Graph

Leben

Shrikhande stammte aus einer Mittelklasse-Familie. Er studierte an der Universität Nagpur mit dem Bachelor-Abschluss 1939 und lehrte dort 1942 bis 1958 Statistik und Mathematik. Er unternahm schon in den 1940er Jahren mehrere lange Reisen um Raj Chandra Bose in Kalkutta zu treffen und fuhr auch zu diesem an die University of North Carolina, um bei ihm 1950 zu promovieren (Construction of partially balanced designs and related problems).[2] Sie arbeiteten danach bis zu Boses Tod eng zusammen. 1951 wurde Shrikhande Assistant Professor an der University of Kansas in Lawrence und 1958 bis 1960 Associate Professor an der University of North Carolina bei Bose. 1960 wurde er Professor an der Banaras Hindu University und 1963 Professor und Leiter der Mathematikfakultät an der Universität Bombay. Außerdem war er Direktor des Centre for Advanced Study in Mathematics in Bombay. 1978 wurde er emeritiert. 1983 bis 1986 war er Direktor des Mehta Research Institute in Allahabad.

Bekannt wurde er, als er 1959 mit Raj Chandra Bose die Eulersche Vermutung (Leonhard Euler 1782) widerlegte, dass keine orthogonalen lateinischen Quadrate der Ordnung $n=4k+2$ existieren (sie fanden ein Gegenbeispiel zur Vermutung für n=22).[3][4] Ihr lateinisches Quadrat wurde auf dem Titel von Scientific American im November 1959 abgebildet. Fast gleichzeitig fand auch Ernest Tilden Parker (1926–1991) in den USA ein Gegenbeispiel für n=10. Das führte zu einer gemeinsamen Arbeit 1960 mit Shrikhande und Bose, in der sie zeigten, dass für alle Ordnungen $n\geq 10$ orthogonale lateinische Quadrate existieren.[5]

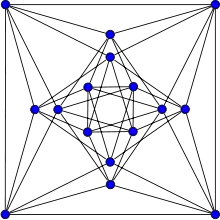
Bekannt ist er auch für Designs in der Versuchsplanung. Der Shrikhande-Graph ist nach ihm benannt und wurde von ihm 1959 entdeckt[6], ein stark-regulärer Graph mit 16 Knoten und 48 Kanten, in der jeder Knoten den Grad 6 hat. Jedes Knotenpaar (ob verbunden oder nicht) hat dort genau zwei weitere Knoten als Nachbarn.[7]

Er war Mitglied der Indian National Science Academy, der Indian Academy of Sciences, des Institute of Mathematical Statistics und des International Statistical Institute. Shrikhande war Gastprofessor an der University of Wisconsin, der Ohio State University, der State University of New York, der Stanford University und der Colorado State University. Außerdem war er in verschiedenen Funktionen mit dem Indian Statistical Institute verbunden.

Sein Sohn Mohan Shrikhande ist Professor für Kombinatorik an der Central Michigan University.

Literatur

Editorial: S. S. Shrikhande and his work. An appreciation, Journal of Statistical Planing and Inference, Band 95, 2001, S. 3–7
Selected Papers of S. S. Shrikhande, 2 Bände, Hrsg. D. S. Meek, R. G. Stanton, Charles Babbage Research Centre, Winnipeg 1985

Einzelnachweise

Sharadchandra Shankar Shrikhande: Nachruf. In: news18.com/news/opinion, abgerufen am 11. Mai 2020.
Sharadchandra Shankar Shrikhande im Mathematics Genealogy Project (englisch)
R. C. Bose, S. S. Shrikhande: On the falsity of Euler´s conjecture about the non-existence of two orthogonal latin squares of order 4t+2. In: Proc. Nat. Acad. Sci. USA. Band 45, 1959, S. 734–737, PMID 16590435, PMC 222625 (freier Volltext) – (englisch).
R. C. Bose and S. S. Shrikhande: On the construction of sets of mutually orthogonal latin squares and the falsity of a conjecture of Euler. In: Trans. Amer. Math. Soc. Band 95, 1960, S. 191–209, doi:10.1090/S0002-9947-1960-0111695-3 (englisch).
R. C. Bose, S. S. Shrikhande, E. T. Parker: Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler's conjecture. In: Canadian Journal of Mathematics. Band 12, 1960, S. 189–, doi:10.4153/CJM-1960-016-5 (englisch, PDF).
Shrikhande, S. S.: The Uniqueness of the $L_{2}$ Association Scheme. In: Ann. Math. Stat. Band 30, 1959, S. 781–798, JSTOR:2237417 (englisch).
Eric Weisstein, Shrikhande Graph

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Sharadchandra Shankar Shrikhande: Nachruf. In: news18.com/news/opinion, abgerufen am 11. Mai 2020.

[2] Sharadchandra Shankar Shrikhande im Mathematics Genealogy Project (englisch)

[3] R. C. Bose, S. S. Shrikhande: On the falsity of Euler´s conjecture about the non-existence of two orthogonal latin squares of order 4t+2. In: Proc. Nat. Acad. Sci. USA. Band 45, 1959, S. 734–737, PMID 16590435, PMC 222625 (freier Volltext) – (englisch).

[4] R. C. Bose and S. S. Shrikhande: On the construction of sets of mutually orthogonal latin squares and the falsity of a conjecture of Euler. In: Trans. Amer. Math. Soc. Band 95, 1960, S. 191–209, doi:10.1090/S0002-9947-1960-0111695-3 (englisch).

[5] R. C. Bose, S. S. Shrikhande, E. T. Parker: Further results on the construction of mutually orthogonal Latin squares and the falsity of Euler's conjecture. In: Canadian Journal of Mathematics. Band 12, 1960, S. 189–, doi:10.4153/CJM-1960-016-5 (englisch, PDF).

[6] Shrikhande, S. S.: The Uniqueness of the $L_{2}$ Association Scheme. In: Ann. Math. Stat. Band 30, 1959, S. 781–798, JSTOR:2237417 (englisch).

[7] Eric Weisstein, Shrikhande Graph