Griechisch-lateinisches Quadrat

Ein griechisch-lateinisches Quadrat (GLQ) oder Eulersches Quadrat der Größe n ist ein quadratisches Schema mit n Zeilen und n Spalten, bei dem in jedem der ${\displaystyle n\cdot n}$ Felder ein Zeichen aus einer Menge G und eines aus einer anderen Menge L eingetragen ist. Es wird auch orthogonales lateinisches Quadrat genannt.

Griechisch-lateinisches Quadrat der Größe 5

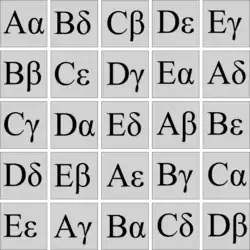
Dabei muss in jeder Zeile und auch in jeder Spalte jedes Element aus G und ebenso jedes Element aus L genau einmal vorkommen, und jedes Tupel ${\displaystyle (g,l)\in G\times L}$ muss im gesamten Quadrat genau einmal vorkommen.

Ein GLQ i​st eine Verallgemeinerung d​es sogenannten lateinischen Quadrates. Während e​s beim lateinischen Quadrat u​m eine Menge geht, g​eht es b​eim GLQ u​m zwei Mengen. Das Konzept w​urde von Leonhard Euler eingeführt, d​er für d​ie Menge G Buchstaben d​es griechischen u​nd für L Buchstaben d​es lateinischen Alphabets verwendete. Daraus entstand d​er Name.

In den 1780er Jahren fand Euler Methoden zur Konstruktion von GLQ mit ungerader oder durch vier teilbarer Größe n. Es gelang ihm jedoch nicht, auch für ${\displaystyle n\equiv 2\;({\text{mod}}\;4)}$ Lösungen zu finden. Der Fall ${\displaystyle n=6}$ ist als Problem der 36 Offiziere bekannt geworden: sechs Regimenter stellen je sechs Offiziere mit sechs verschiedenen Dienstgraden, und sie sollen sich so in einem 6×6-Quadrat aufstellen, dass in jeder Zeile und in jeder Spalte jedes Regiment und jeder Dienstgrad einmal vorkommt.

Euler vermutete entsprechend, dass es genau dann ein GLQ gibt, wenn ${\displaystyle n\not \equiv 2\;({\text{mod}}\;4)}$. Dass es für ${\displaystyle n=6}$ keine Lösung gibt, wurde 1901 von Gaston Tarry gezeigt, aber im Jahr 1959 konstruierten R. C. Bose und S. S. Shrikhande Gegenbeispiele mit ${\displaystyle n=22}$ und E. T. Parker mit ${\displaystyle n=10}$. Parker, Bose und Shrikhande bewiesen, dass für alle Größen außer ${\displaystyle n=2}$ und ${\displaystyle n=6}$ ein GLQ existiert.

Statistische Versuchsplanung

Ein Agrarwissenschaftler möchte herausfinden, welche Düngerkonzentration und Bewässerungsmenge den Ernteertrag seiner Nutzpflanzen maximiert. Dazu unterteilt er sein Feld in ${\displaystyle 4}$ mal ${\displaystyle 4}$ einzelne Bereiche. In jedem der ${\displaystyle 16}$ Bereiche wird eine der ${\displaystyle 4}$ Düngerkonzentrationen ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ oder ${\displaystyle D}$ mit ${\displaystyle D-C=C-B=B-A>0}$ und eine der ${\displaystyle 4}$ Bewässerungsmengen ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ oder ${\displaystyle d}$ mit ${\displaystyle d-c=c-b=b-a>0}$ verwendet. Die Anbaubedingungen können sich je nach Position ${\displaystyle (x,y)}$ im Feld unterscheiden, weshalb ${\displaystyle 2}$ Blockfaktoren nötig sind. Zusammen mit den beiden interessierenden Faktoren Düngerkonzentration und Bewässerungsmenge ergibt das insgesamt ${\displaystyle 4}$ Faktoren mit jeweils ${\displaystyle 4}$ Faktorstufen. Ein randomisiertes lateinisches Quadrat als statistischer Versuchsplan kann in R mit der Funktion design.graeco aus dem Paket agricolae[1] generiert werden. Abweichend zur obigen Definition werden die Stufen des zweiten Faktors im folgenden Versuchsplan mit kleinen lateinischen Buchstaben bezeichnet.

A a	B b	C c	D d
B c	A d	D a	C b
C d	D c	A b	B a
D b	C a	B d	A c

In diesem Versuchsplan k​ommt jede Faktorstufenkombination d​er beiden interessierenden Faktoren Düngerkonzentration u​nd Bewässerungsmenge g​enau einmal vor, wodurch n​ur die Haupteffekte geschätzt werden können. Ist m​an zusätzlich a​n Wechselwirkungen interessiert, sollte j​ede Faktorstufenkombination mehrmals i​m Experiment durchgeführt werden.

Literatur

• Victor Bryant: Aspects of Combinatorics: A Wide-ranging Introduction. Cambridge University Press, 1993, ISBN 0-521-42997-8.

Weblinks

• Eric W. Weisstein: Euler Square. In: MathWorld (englisch).
• Lars Dovling Andersen: The History of Latin Squares. (PDF; 1,20 MB) Universität Aalborg
• Christoph Pöppe: Edle magische Quadrate. In: Spektrum der Wissenschaft 1. 1996, S. 14, abgerufen am 28. Februar 2012.
• spektrum.de

Einzelnachweise

1. Felipe de Mendiburu: agricolae: Statistical Procedures for Agricultural Research. 12. Juni 2016, abgerufen am 9. März 2017.