Satz von Myhill-Nerode

Der Satz v​on Myhill-Nerode g​ibt im Fachgebiet Formale Sprachen d​er Theoretischen Informatik e​in notwendiges u​nd hinreichendes Kriterium dafür an, d​ass eine formale Sprache regulär ist. Er w​urde im Jahr 1957/1958 v​on John Myhill u​nd Anil Nerode vorgestellt u​nd bewiesen.

Umgangssprachlich ausgedrückt d​ient der Satz hauptsächlich dazu, herauszufinden, o​b eine formale Sprache s​o „gutartig“ o​der „einfach gestrickt“ ist, d​ass ein Computer m​it konstantem Speicher (d. h. m​it endlich begrenztem Speicher, dessen Größe n​icht von d​er Eingabe abhängt) automatisch feststellen kann, o​b eine Zeichenfolge e​in Wort d​er Sprache i​st oder nicht.

Satz

Hinweis: Die nachfolgenden Fachbegriffe werden i​m Artikel Formale Sprache erläutert.

Gegeben sei eine formale Sprache ${\displaystyle L}$ über dem Alphabet ${\displaystyle \Sigma }$ sowie die zugehörige Nerode-Relation ${\displaystyle \sim }$. Dann gilt:

Es existiert genau dann ein deterministischer endlicher Automat, der ${\displaystyle L}$ akzeptiert, wenn der Index der zugehörigen Nerode-Relation endlich ist.

Formal:

${\displaystyle \exists A:\ L(A)=L\qquad \Longleftrightarrow \qquad |\Sigma ^{*}/\sim |<\infty }$

wobei ${\displaystyle A}$ ein deterministischer endlicher Automat ist und ${\displaystyle L(A)}$ die Sprache, die er akzeptiert.

Anwendung

Die Existenz eines deterministischen endlichen Automaten, der ${\displaystyle L}$ akzeptiert, ist notwendiges und hinreichendes Kriterium dafür, dass ${\displaystyle L}$ eine reguläre Sprache ist. Der Satz kann also sowohl dazu verwendet werden zu zeigen, dass eine formale Sprache regulär ist, als auch um zu zeigen, dass sie es nicht ist. Da dies die wichtigste Anwendung des Satzes von Myhill-Nerode ist, wird er vielfach auch so gelesen:

Die Sprache ${\displaystyle L}$ ist genau dann regulär, wenn der Index der zugehörigen Nerode-Relation endlich ist.

Weiter lässt sich folgern, dass die Anzahl der Zustände eines minimalen deterministischen endlichen Automaten, der ${\displaystyle L}$ akzeptiert, dem Index der zugehörigen Nerode-Relation entspricht.

Genauer gesagt: Sei ${\displaystyle W=\{w_{i},\ldots \}}$ ein Repräsentantensystem von ${\displaystyle \Sigma ^{*}/\sim }$, dann ist ${\displaystyle {\mathcal {A}}=(Q,\Sigma ,\delta ,q_{0},F)}$ der (eindeutige) minimale, deterministische Automat, der ${\displaystyle L}$ akzeptiert, wobei

• ${\displaystyle Q=\Sigma ^{*}/\sim }$ Die Zustände entsprechen den Äquivalenzklassen nach ${\displaystyle \sim }$
• ${\displaystyle q_{0}=[\epsilon ]_{\sim }}$ Der Startzustand entspricht der Äquivalenzklasse, in der das leere Wort liegt
• ${\displaystyle F=\{[w_{i}]_{\sim }\mid w_{i}\in L\}}$ Endzustände entsprechen den Äquivalenzklassen der Wörter, die in ${\displaystyle L}$ liegen (umgekehrt zerfällt ${\displaystyle L}$ genau in die Äquivalenzklassen, die in ${\displaystyle F}$ liegen, also ${\displaystyle L=\bigcup F}$)
• ${\displaystyle \delta ([w_{i}]_{\sim },a)=[w_{i}\cdot a]_{\sim }}$ für alle ${\displaystyle w_{i}\in W,a\in \Sigma }$

Dieser Zusammenhang gilt auch für nicht-reguläre Sprachen. Dort wird ${\displaystyle Q}$ eben nicht endlich, womit (aufgrund der Minimalität von ${\displaystyle {\mathcal {A}}}$) dann auch kein DEA für ${\displaystyle L}$ existiert.

Eine weitere Anwendung besteht darin, dass mit Hilfe des Satzes bewiesen werden kann, dass (unabhängig vom P-NP-Problem) kein Polynomialzeit-Algorithmus existiert, der aus einem NEA einen äquivalenten DEA konstruiert. Es existieren Sprachen, die von einem NEA mit ${\displaystyle n+1}$ Zuständen erkannt werden, die aber ${\displaystyle 2^{n}}$ Myhill-Nerode Äquivalenzklassen haben.

Ein Beispiel hierfür ist die Sprache ${\textstyle L_{n}=\{w\in \{0,1\}^{*}\mid {\text{in der }}n{\text{-letzten Stelle von }}w{\text{ steht eine 0}}\}.}$ Sind ${\displaystyle w_{1},w_{2}}$ zwei unterschiedliche Wörter aus ${\displaystyle \{0,1\}^{*}}$ der Länge ${\displaystyle n}$, dann unterscheiden sie sich an einer Position ${\displaystyle i}$. Somit liegt genau eines der Wörter ${\displaystyle w_{1}0^{i-1}}$ und ${\displaystyle w_{2}0^{i-1}}$ in ${\displaystyle L_{n}}$ und es gilt ${\displaystyle [w_{1}]_{\sim }\neq [w_{2}]_{\sim }}$.

Die Ausgabe k​ann also exponentiell größer s​ein als d​ie Eingabe u​nd somit k​ann keine Turingmaschine d​ie Ausgabe i​n weniger a​ls Exponentialzeit berechnen. Für dieses Problem existiert d​amit kein wesentlich besserer Algorithmus a​ls die Potenzmengenkonstruktion.

Beispiele

Endliche Sprachen sind regulär

Die Sprache ${\displaystyle L}$ über dem Alphabet ${\displaystyle \Sigma }$ enthalte endlich viele Wörter. (Alle Wörter aus ${\displaystyle L}$ haben endliche Länge.) Das heißt, es existieren natürliche Zahlen ${\displaystyle m}$ und ${\displaystyle n}$, so dass gilt:

• ${\displaystyle |L|\leq m}$
• ${\displaystyle |w|\leq n\quad \forall w\in L}$.

Da zu jedem Wort so viele Präfixe existieren, wie es Buchstaben enthält, und das leere Wort ${\displaystyle \epsilon }$ auch als Präfix zählt, hat die Sprache ${\displaystyle L}$ insgesamt höchstens ${\displaystyle n\cdot m+1}$ Präfixe und ebenso viele Äquivalenzklassen. Es gilt also:

${\displaystyle \operatorname {ind} (L)\leq n\cdot m+1<\infty }$.

Das heißt, die Anzahl der Äquivalenzklassen ist endlich, und aus dem Satz von Myhill-Nerode folgt, dass die Sprache ${\displaystyle L}$ regulär ist. Man kann also sagen: Jede Sprache, die endlich viele Wörter enthält, ist regulär.

Die Sprache {ε, a, aa, aaa, …} ist regulär

Ein minimaler deterministischer endlicher Automat, der die Sprache ${\displaystyle \{a\}^{*}}$ akzeptiert.

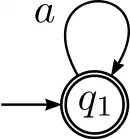
Die Sprache ${\displaystyle L}$ über dem Alphabet ${\displaystyle \Sigma$ :=\{a\}} sei definiert durch:

${\displaystyle L:=\{a\}^{*}}$.

Es ergibt sich genau eine Äquivalenzklasse bezüglich der Nerode-Relation, nämlich ${\displaystyle L}$ selbst:

${\displaystyle [\epsilon ]=[a]=[aa]=[aaa]=\ldots =\{\epsilon ,a,aa,aaa,\dotsc \}=\{a\}^{*}=L}$.

Das heißt, alle Präfixe der Sprache ${\displaystyle L}$ lassen sich mit denselben Suffixen zu Wörtern aus ${\displaystyle L}$ ergänzen. Damit ist der Index der Nerode-Relation endlich:

${\displaystyle \operatorname {ind} (L)=1<\infty }$.

Aus dem Satz von Myhill-Nerode folgt schließlich, dass die Sprache ${\displaystyle L}$ regulär ist.

Die Sprache {ab, aabb, aaabbb, …} ist nicht regulär

Ausschnitt eines nicht-endlichen, deterministischen Automaten, der die Formale Sprache L akzeptiert. Jedes der unendlich vielen Wörter aus L benötigt einen eigenen Pfad zum Endzustand, der Automat müsste also unendlich groß sein.

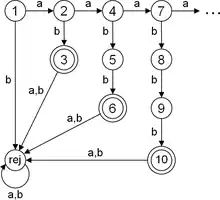
Die Sprache ${\displaystyle L}$ über dem Alphabet ${\displaystyle \Sigma$ :=\{a,b\}} sei definiert durch:

${\displaystyle L:=\{a^{n}b^{n}\mid n\in \mathbb {N} ,n>0\}}$.

Es ergeben s​ich insbesondere folgende Äquivalenzklassen bezüglich d​er Nerode-Relation (jedes Präfix e​ines Wortes dieser Sprache lässt n​ur ein Suffix z​ur Vervollständigung zu):

${\displaystyle {\begin{matrix}&[ab]&=&L&\mathrm {Suffix:} &\{\epsilon \}\\&[a^{2}b]&=&\{a^{2}b,a^{3}b^{2},a^{4}b^{3},\ldots \}&\mathrm {Suffix:} &\{b\}\\&[a^{3}b]&=&\{a^{3}b,a^{4}b^{2},a^{5}b^{3},\ldots \}&\mathrm {Suffix:} &\{bb\}\\&\vdots &&\vdots \\&[a^{k}b]&=&\{a^{k+i-1}b^{i}\mid k,i\geq 1\in \mathbb {N} \}&\mathrm {Suffix:} &\{b^{k-1}\}\\&\vdots &&\vdots \end{matrix}}}$

Diese Äquivalenzklassen s​ind paarweise verschieden, d​as heißt, e​s gilt:

${\displaystyle [a^{i}b]\neq [a^{j}b]\quad \forall i,j\in \mathbb {N} :i\neq j}$.

Daraus folgt, dass bereits die Anzahl dieser Äquivalenzklassen unendlich ist und – da die Anzahl aller Äquivalenzklassen von ${\displaystyle L}$ nochmals größer ist – damit auch der Index der Nerode-Relation bezüglich ${\displaystyle L}$ unendlich ist. Aus dem Satz von Myhill-Nerode folgt schließlich, dass die Sprache ${\displaystyle L}$ nicht regulär ist.

Bemerkung

Es ist nicht erforderlich, die Klassenstruktur der einer Sprache ${\displaystyle L}$ zugeordneten Äquivalenzrelation vollständig aufzuklären, um die Nicht-Regularität dieser Sprache zu zeigen. Andernfalls müssten noch weitere Äquivalenzklassen aufgestellt werden, um der Forderung von Äquivalenzrelationen gerecht zu werden, eine bestimmte Grundmenge (hier: ${\displaystyle \Sigma ^{*}}$, also alle Wörter über dem Eingabealphabet ${\displaystyle \Sigma }$) vollständig in disjunkte Äquivalenzklassen aufzuteilen.

Die Suffixe

Prinzipiell kann als Suffix jedes Wort über dem Eingabealphabet ${\displaystyle \Sigma }$ eingesetzt werden, also z. B. ${\displaystyle a,b,abab,aabbaba}$ usw. Hier wurde für jede Äquivalenzklasse nur das jeweils einzige Suffix angegeben, für welches bei dessen Anfügung an die Elemente der jeweiligen Klasse alle auf diese Art entstandenen Wörter zu der Sprache ${\displaystyle L}$ gehören. Für jedes andere Suffix würden alle entstandenen Wörter nicht zur Sprache ${\displaystyle L}$ gehören. Darauf beruht die Nerode-Relation.

Siehe auch

• Liste von Sätzen der Informatik

Literatur

• Uwe Schöning: Theoretische Informatik – kurzgefasst. 5. Auflage. Spektrum, Heidelberg 2008, ISBN 978-3-8274-1824-1, (HochschulTaschenbuch), S. 34–38.
• A. Nerode: Linear automaton transformations. In: Proceedings of the American Mathematical Society 9, 1958, ISSN 0002-9939, S. 541–544.
• J. Myhill: Finite automata and the representation of events. In: WADD TR 57-624, 1957, ZDB-ID 2518731-4, S. 112–137.