Satz von Beltrami-Enneper

Der Satz v​on Beltrami-Enneper (nach Eugenio Beltrami[1] u​nd Alfred Enneper[2]) i​st ein Resultat a​us der Differentialgeometrie d​er Flächen.

Aussage

Das Quadrat d​er Torsion e​iner Asymptotenlinie i​st gleich d​er negativen gaußschen Krümmung d​er Fläche, i​n der s​ich die Kurve bewegt, sofern d​ie Krümmung d​er Kurve selbst n​icht verschwindet.[3][4] Eine Kurve a​uf einer Fläche heißt Asymptotenlinie, w​enn die zweite Fundamentalform d​er Fläche entlang d​er Kurve verschwindet. Insbesondere i​st die gaußsche Krümmung i​n jedem Punkt e​iner Asymptotenlinie nichtpositiv.

Anwendungsbeispiel

Aus dem Satz von Beltrami-Enneper folgt[5]: Ist ${\displaystyle X}$ eine reguläre Fläche, die eine Gerade ${\displaystyle L=\{\gamma (t)\}}$ enthält (dabei ${\displaystyle \gamma }$ Parametrisierung nach der Bogenlänge), und ${\displaystyle \lambda (t)}$ ein an ${\displaystyle X}$ tangentiales, auf ${\displaystyle L}$ orthogonales Einheitsvektorfeld entlang ${\displaystyle \gamma (t)}$, dann ist die Krümmung von ${\displaystyle X}$ in ${\displaystyle \gamma (t)}$ gleich

${\displaystyle -\left|{\frac {d\lambda (t)}{dt}}\right|^{2}}$

Einschaliges Hyperboloid

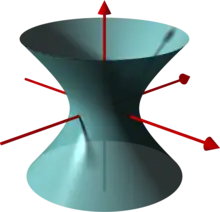
Sei ${\displaystyle X=\{x^{2}+y^{2}-z^{2}=1\}}$ das einschalige Hyperboloid und

${\displaystyle \gamma (t)=\left(1,{\frac {t}{\sqrt {2}}},{\frac {t}{\sqrt {2}}}\right),\lambda (t)={\frac {1}{\sqrt {1+t^{2}}}}\cdot \left(-t,{\frac {1}{\sqrt {2}}},-{\frac {1}{\sqrt {2}}}\right)\,.}$

Dann ist

${\displaystyle {\frac {d\lambda (t)}{dt}}={\frac {1}{(1+t^{2})^{3/2}}}\cdot \left(-1,-{\frac {t}{\sqrt {2}}},{\frac {t}{\sqrt {2}}}\right)}$

und damit

${\displaystyle -\left|{\frac {d\lambda (t)}{dt}}\right|^{2}={\frac {-1}{(1+t^{2})^{2}}}=K\,.}$

Einzelnachweise

1. Eugenio Beltrami: Dimostrazione di due formole del Sig. Bonnet. In: Giornale di Matematiche. 4, 1866, ZDB-ID 281094-3, S. 123–127 (Auch in: Eugenio Beltrami: Opere matematiche. Band 1. Hoepli, Mailand 1902, S. 297–301), Online.
2. Alfred Enneper: Über asymptotische Linien. In: Nachrichten von der Georg-Augusts-Universität und der Königl. Gesellschaft der Wissenschaften zu Göttingen. 12, 1870, ZDB-ID 502554-0, S. 493–510, (Resultat ist formuliert auf S. 499), Online
3. W. Blaschke, K. Leichtweiß: Elementare Differentialgeometrie (= Vorlesungen über Differentialgeometrie. 1 = Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. 1). 5. vollständig neubearbeitete Auflage. Springer-Verlag, Berlin u. a. 1973, ISBN 3-540-05889-3, § 56, S. 133f.
4. Wolfgang Kühnel: Differentialgeometrie. Kurven – Flächen – Mannigfaltigkeiten. 5. aktualisierte Auflage. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1233-9, Satz 3.19, S. 57.
5. Victor Andreevich Toponogov: Differential geometry of curves and surfaces. A concise guide. Birkhäuser, Boston u. a. 2006, ISBN 0-8176-4384-2, Theorem 2.7.6.