Südpolsatz

Der Südpolsatz i​st ein geometrischer Satz a​us der Dreieckslehre. Er besagt, d​ass sich i​n einem Dreieck d​ie Mittelsenkrechte (Streckensymmetrale) e​iner Seite u​nd die Winkelhalbierende (Winkelsymmetrale) d​urch die gegenüberliegende Ecke i​mmer auf d​em Umkreis schneiden. Der Schnittpunkt w​ird auch Südpol genannt.

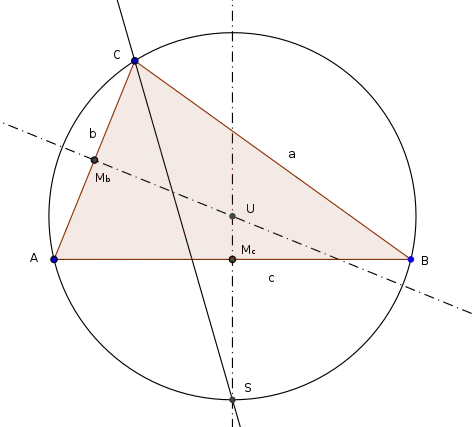
Beweis

1. Der Satz soll für die Mittelsenkrechte ${\displaystyle m_{c}}$ und die Winkelhalbierende ${\displaystyle w_{\gamma }}$ begründet werden. S sei definiert als derjenige Schnittpunkt der Mittelsenkrechten ${\displaystyle m_{c}}$ mit dem Umkreis, der nicht auf der gleichen Seite von AB liegt wie die Ecke C. Ist U der Umkreismittelpunkt, so ist der Winkel ACS halb so groß wie der Winkel AUS, da es sich um den Umfangswinkel (Peripheriewinkel) und Mittelpunktswinkel (Zentriwinkel) über dem Kreisbogen AS handelt. Entsprechend ist der Winkel SCB halb so groß wie der Winkel SUB. Da die Winkel AUS und SUB aus Symmetriegründen gleich groß sind, müssen auch die Winkel ACS und SCB gleich groß sein. Mit anderen Worten: S muss auf der Winkelhalbierenden des Winkels ${\displaystyle \gamma =\angle ACB}$ liegen. Der Schnittpunkt der Mittelsenkrechten und der Winkelhalbierenden muss also mit S übereinstimmen und folglich auf dem Umkreis liegen.
2. Da S auf der Mittelsenkrechten von AB liegt, müssen aus Symmetriegründen die Strecken AS und BS gleich lang sein. Nach dem Umfangswinkelsatz müssen die Winkel über einer gleich langen Sehne gleich groß sein, also sind die Winkel in C über den Sehnen AS und BS auch gleich groß. Und deshalb ist CS die Winkelhalbierende in C, die sich mit der Mittelsenkrechten auf dem Umkreis schneidet.

Literatur

• H.K. Dass, Rama Verma, Bhagwat S. Sharma: S.Chand’S Mathematics For Class IX Term II. S. Chand Publishing, 2011, ISBN 9788121938464, S. 165–166

Weblinks

• Franz Hofbauer: Geometrie und Lineare Algebra für das Lehramt. Skript, Uni Wien, Seite 24, Satz 33 (enthält ähnlichen Beweis)
• Lucas Mann: Skript zum MSG-Zirkel. Skript der mathematischen Schülergesellschaft Leonard Euler, Seite 51, Aufgabe 5.16
• Dörte Haftendorn: Südpolsatz – Zeichnung und Beweis (pdf)
• Walter Fendt: Der Südpolsatz (interaktive Illustration)