Rugate-Spiegel

Ein Rugate-Spiegel oder auch Rugate-Filter ist ein dielektrischer Spiegel, der einen bestimmten Wellenlängenbereich von Licht selektiv reflektiert. Dieser Effekt wird durch eine periodische, stetige Änderung des Brechungsindex, abhängig von der Dicke des Spiegels, erzielt. Ein bestimmter Wellenlängenanteil von Licht kann sich nicht im Rugate-Spiegel ausbreiten und wird reflektiert.

Rugate-Filter hergestellt aus porösem Siliciumcarbid.[1]

Das Wort „rugate“ leitet sich im Englischen aus dem Wort corrugated (dt. ‚gewellt‘) ab, mit dem in der Natur vorkommende gewellte Strukturen (englisch corrugated structures) bezeichnet werden, die ebenfalls selektiv bestimmte Wellenlängenanteile von Licht reflektieren.[2] Ein Beispiel dafür sind die Flügel des Morphofalters.[3]

Charakteristika

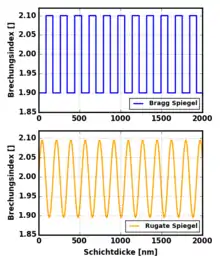
Brechungsindex-Profile eines Bragg- und Rugate-Spiegels mit maximaler Reflektivität bei 700 nm.

Reflexions-Spektren eines Bragg und Rugate-Spiegels bei senkrechtem Lichteinfall mit maximaler Reflektivität bei 700 nm.

Bei Rugate-Spiegeln variiert der Brechungsindex als Funktion der Dicke des Spiegels periodisch und stetig. Dies ist ähnlich wie beim Bragg-Spiegel mit dem Unterschied, dass dort das Brechungsindexprofil unstetig ist. Der Vergleich des Brechungsindexprofils eines Rugate- und Bragg-Spiegels ist in der Grafik rechts veranschaulicht. Beim Bragg-Spiegel sind die unstetigen Übergänge für Reflexion von einfallendem Licht verantwortlich, während bei Rugate-Spiegeln an jeder Position einfallendes Licht reflektiert wird. Gemäß den Fresnel-Gleichungen ist der Reflexionskoeffizient jedoch dort am größten wo auch die größte Änderung des Brechungsindex stattfindet. Beim Rugate-Spiegel sind dies die Wendepunkte im Brechungsindexprofil. Mit Hilfe der Theorie des Bragg-Spiegels lässt sich somit jene Wellenlänge berechnen, bei der die Reflexion eines Rugate-Spiegels am größten ist. Für eine alternierende Abfolge im Bragg-Spiegel ergibt sich das Maximum der Reflexion bei einer Wellenlänge $\lambda _{0}$ zu:

n_{L}d_{L}+n_{H}d_{H}={\frac {\lambda _{0}}{2}}

In dieser Gleichung stehen $n_{L}$ und $n_{H}$ für den hohen und niedrigen Brechungsindex im Bragg-Spiegel während $d_{L}$ und $d_{H}$ die jeweiligen physikalischen Dicken dieser Lagen kennzeichnen. Für den allgemeineren Fall, dass sich der Brechungsindex stetig ändert, kann man die vorherige Gleichung umschreiben:

{\frac {\int _{0}^{d}{n(x)}\mathrm {d} x}{d}}d=\left\langle n\right\rangle d={\frac {\lambda _{0}}{2}}

Auf der linken Seite steht das Integral über den Brechungsindex über eine Periode des Brechungsindexprofiles $n(x)$ dividiert durch die Periodenlänge $d$ . Dieser Term entspricht dem Mittelwert des Brechungsindexprofiles[4]. Man kann sich von der Richtigkeit dieser Gleichung überzeugen, indem man das Integral für ein diskretes Brechungsindexprofil löst und die Periode eines Bragg-Spiegels $d=d_{H}+d_{L}$ einsetzt.

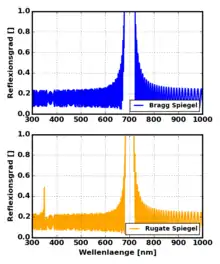
Im Bild rechts sind die mit Hilfe der Matrix-Transfer-Methode berechneten Reflexionsspektren für die eingangs dargestellten Brechungsindexprofile eines Bragg- sowie Rugate-Spiegels abgebildet. Man sieht, dass beide Spiegel ihre maximale Reflektivität bei 700 nm aufweisen, wobei der Rugate-Spiegel eine geringere Bandbreite aufweist. Aus diesem Grund werden Rugate-Spiegel oft als optische Notch-Filter verwendet. Weiters sieht man im Spektrum des Rugate-Filters einen kleineren Peak beim $\lambda _{0}/2$ . Dieser Peak ist im Spektrum des Bragg-Spiegels nicht zugegen, da es aufgrund seines diskreten Schichtsystems zu destruktiver Interferenz bei dieser Wellenlänge kommt. Bragg-Spiegel weisen aber Nebenmaxima bei Wellenlängen von $\lambda _{0}/(2n-1)$ auf, die unerwünscht sein können wenn man nur möglichst eine bestimmte Wellenlänge herausfiltern möchte. Rugate-Spiegel sind hier besser geeignet, da das sinusförmige Brechungsindex-Profil Anti-Reflex-Eigenschaften ähnlich wie bei schwarzem Silicium aufweist. Dadurch sind die Nebenmaxima in ihrer Intensität verringert[4].

Herstellung

Rugate-Spiegel können mittels Sputtern[5] und chemischer Gasphasenabscheidung[6] hergestellt werden. Eine besondere Herausforderung ist dabei die Realisierung des stetigen Brechungsindex-Profiles. Um dieses zu erreichen muss sich auch die chemische Zusammensetzung des Spiegels stetig als Funktion der Schichtdicke ändern. Man kann dies durch kontinuierliche Veränderung der Gaszusammensetzung bei diesen Abscheideprozessen erreichen. Eine weitere Möglichkeit zur Herstellung von Rugate-Spiegeln ist elektrochemisches Porösizieren von Silicium. Dabei wird die Stromdichte während des Ätzvorganges so gewählt, dass die resultierende Porosität und somit der Brechungsindex sinusförmig mit der Schichtdicke variiert.[7]

Einzelnachweise

Markus Leitgeb, Christopher Zellner, Michael Schneider, Ulrich Schmid: Porous single crystalline 4H silicon carbide rugate mirrors. In: APL Materials. 5, Nr. 10, 2017, S. 106106. doi:10.1063/1.5001876.
H. A. Macleod: Thin-Film Optical Filters. 3. Auflage. Institute of Physics Publishing, Bristol/Philadelphia 2001, ISBN 0-7503-0688-2 (Erstausgabe: 1986).
Radislav Potyrailo, Ravi K. Bonam, John G. Hartley, Timothy A. Starkey, Peter Vukusic, Milana Vasudev, Timothy Bunning, Rajesh R. Naik, Zhexiong Tang, Manuel A. Palacios, Michael Larsen, Laurie A. Le Tarte, James C. Grande, Sheng Zhong, Tao Deng: Towards outperforming conventional sensor arrays with fabricated individual photonic vapour sensors inspired by Morpho butterflies. In: Nature Communications. 6, 2014, S. 7959. doi:10.1038/ncomms8959.
Olaf Stenzel: Optical Coatings. 3. Auflage. Springer Science & Business, Heidelberg 2014, ISBN 978-3-642-54063-9 (Erstausgabe: 2014).
H. Bartzsch, S. Lange, P. Frach, K. Goedicke: Graded refractive index layer systems for antireflective coatings and rugate filters deposited by reactive pulse magnetron sputtering. In: Surface and Coatings Technology. Band 180, 2004, S. 616–620, doi:10.1016/j.surfcoat.2003.10.105.
S. Lim, J. H. Ryu, J. F. Wager, T. K. Plant: Rugate filters grown by plasma-enhanced chemical vapor deposition. In: Thin Solid Films. Band 245, Nr. 1–2, 1994, S. 141–145, doi:10.1016/0040-6090(94)90889-3.
Claudia Pacholski: Photonic Crystal Sensors Based on Porous Silicon. In: Sensors. Band 13, Nr. 4, 9. April 2013, S. 4694–4713, doi:10.3390/s130404694.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Markus Leitgeb, Christopher Zellner, Michael Schneider, Ulrich Schmid: Porous single crystalline 4H silicon carbide rugate mirrors. In: APL Materials. 5, Nr. 10, 2017, S. 106106. doi:10.1063/1.5001876.

[Macleod-2] H. A. Macleod: Thin-Film Optical Filters. 3. Auflage. Institute of Physics Publishing, Bristol/Philadelphia 2001, ISBN 0-7503-0688-2 (Erstausgabe: 1986).

[3] Radislav Potyrailo, Ravi K. Bonam, John G. Hartley, Timothy A. Starkey, Peter Vukusic, Milana Vasudev, Timothy Bunning, Rajesh R. Naik, Zhexiong Tang, Manuel A. Palacios, Michael Larsen, Laurie A. Le Tarte, James C. Grande, Sheng Zhong, Tao Deng: Towards outperforming conventional sensor arrays with fabricated individual photonic vapour sensors inspired by Morpho butterflies. In: Nature Communications. 6, 2014, S. 7959. doi:10.1038/ncomms8959.

[stenzel-4] Olaf Stenzel: Optical Coatings. 3. Auflage. Springer Science & Business, Heidelberg 2014, ISBN 978-3-642-54063-9 (Erstausgabe: 2014).

[5] H. Bartzsch, S. Lange, P. Frach, K. Goedicke: Graded refractive index layer systems for antireflective coatings and rugate filters deposited by reactive pulse magnetron sputtering. In: Surface and Coatings Technology. Band 180, 2004, S. 616–620, doi:10.1016/j.surfcoat.2003.10.105.

[6] S. Lim, J. H. Ryu, J. F. Wager, T. K. Plant: Rugate filters grown by plasma-enhanced chemical vapor deposition. In: Thin Solid Films. Band 245, Nr. 1–2, 1994, S. 141–145, doi:10.1016/0040-6090(94)90889-3.

[7] Claudia Pacholski: Photonic Crystal Sensors Based on Porous Silicon. In: Sensors. Band 13, Nr. 4, 9. April 2013, S. 4694–4713, doi:10.3390/s130404694.