Riemannsche Holonomie

Der mathematische Begriff d​er Riemannschen Holonomiegruppe o​der Riemannschen Holonomie bezeichnet i​n der Differentialgeometrie d​ie Gruppe linearer Transformationen, d​ie durch d​en Paralleltransport v​on Vektoren entlang geschlossener Kurven induziert wird.

Paralleltransport entlang einer geschlossenen Kurve auf der Sphäre

Definition

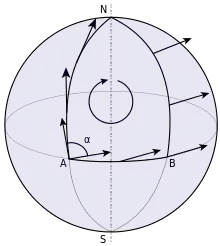
Sei ${\displaystyle (M,g)}$ eine Riemannsche Mannigfaltigkeit. Der Levi-Civita-Zusammenhang definiert den Paralleltransport auf ${\displaystyle M}$. Für jede geschlossene Kurve

${\displaystyle \gamma \colon \left[0,1\right]\to M}$

mit ${\displaystyle \gamma (0)=\gamma _{1}=x_{0}}$ definiert der Paralleltransport eine lineare Abbildung

${\displaystyle H_{\gamma }\colon T_{x_{0}}M\to T_{x_{0}}M}$.

Als (Riemannsche) Holonomiegruppe ${\displaystyle Hol(M,g)}$ von ${\displaystyle (M,g)}$ bezeichnet man die Gruppe aller invertierbaren linearen Abbildungen

${\displaystyle A\in GL(T_{x_{0}}M)}$,

für die es eine geschlossene Kurve ${\displaystyle \gamma }$ mit ${\displaystyle A=H_{\gamma }}$ gibt. Wegen

${\displaystyle H_{\gamma _{1}*\gamma _{2}}=H_{\gamma _{2}}\circ H_{\gamma _{1}}}$ und ${\displaystyle H_{c_{x_{0}}}=Id}$

ist ${\displaystyle Hol(M,g)}$ tatsächlich eine Gruppe.

Zerlegbarkeit von Holonomiedarstellungen

Zerlegungssatz v​on de Rham: Die Holonomiedarstellung e​iner einfach zusammenhängenden Riemannschen Mannigfaltigkeit i​st genau d​ann reduzibel, w​enn die Metrik l​okal ein Produkt ist. Falls d​ie Mannigfaltigkeit geodätisch vollständig ist, m​uss die Metrik s​ogar global e​ine Produktmetrik sein.

Klassifikation irreduzibler Holonomiedarstellungen

Berger-Liste: Die Holonomiegruppe einer einfach zusammenhängenden, irreduziblen, nicht-symmetrischen Riemannschen ${\displaystyle n}$-Mannigfaltigkeit ist eine der folgenden:

• ${\displaystyle SO(n)}$
• ${\displaystyle U(m)}$ mit ${\displaystyle n=2m,m\geq 2}$ (Kählermannigfaltigkeiten)
• ${\displaystyle SU(m)}$ mit ${\displaystyle n=2m,m\geq 2}$ (Calabi-Yau-Mannigfaltigkeiten)
• ${\displaystyle Sp(m)}$ mit ${\displaystyle n=4m,m\geq 2}$ (Hyperkählermannigfaltigkeiten)
• ${\displaystyle Sp(m)Sp(1)}$ mit ${\displaystyle n=4m,m\geq 2}$
• ${\displaystyle G_{2}}$ mit ${\displaystyle n=7}$
• ${\displaystyle Spin(7)}$ mit ${\displaystyle n=8}$

Bergers Liste der möglichen Holonomiegruppen enthielt ursprünglich noch ${\displaystyle Spin(9)}$ mit ${\displaystyle n=16}$, diese Möglichkeit konnte 1968 von Alexeevsky ausgeschlossen werden.

Die Holonomiegruppen symmetrischer Räume waren bereits von Cartan klassifiziert worden. Für einen einfach zusammenhängenden, irreduziblen symmetrischen Raum ${\displaystyle G/H}$ ist die Holonomiegruppe isomorph zu ${\displaystyle H}$.

Spezielle Holonomie: Als Mannigfaltigkeiten spezieller Holonomie bezeichnet man Riemannsche Mannigfaltigkeiten, deren Holonomiegruppe eine echte Untergruppe von ${\displaystyle SO(n)}$ ist, also die Fälle 2-7 in Bergers Liste sowie Produkte, in denen mindestens einer der Faktoren in einen der Fälle 2-7 fällt.

Literatur

• G. de Rham: Sur la réductibilité d’un espace de Riemann, Comm. Math. Helv. 26 (1952), 328–344.
• M. Berger: Sur les groupes d'holonomie homogène des variétés à connexion affine et des variétés riemanniennes, Bull. Soc. Math. France 83 (1955), 279–330.

Weblinks

• J. Gross: What is ... Riemannian holonomy?, Notices of the AMS 65 (2018), 795–796.