Reibungskoeffizient

Der Reibungskoeffizient, auch Reibungszahl genannt (Formelzeichen µ oder f), ist eine Größe der Dimension Zahl für das Verhältnis der Reibungskraft zur Anpresskraft zwischen zwei Körpern. Der Begriff gehört zum Fachgebiet der Tribologie.

Physikalische Bedeutung

Bei der Angabe eines Reibungskoeffizienten wird zwischen Gleitreibung und Haftreibung unterschieden: Bei der Gleitreibung bewegen sich die Reibflächen relativ zueinander, während sie dies bei der Haftreibung nicht tun. Im Fall der coulombschen Reibung ist der Gleitbeiwert konstant. In der Praxis ist eine entsprechende Temperatur-, Geschwindigkeits- und Druckabhängigkeit zu erkennen, welche auf einen Einfluss der Oberflächenänderung und Beschaffenheit der niemals ideal ebenen Fläche hindeutet (aber nicht auf den Reibwert selbst) und damit die Materialeigenschaft scheinbar beeinflusst.

Gemessen wird der Reibungskoeffizient bei Metallen an polierten Oberflächen, um eine mechanische Verzahnung (Formschluss) weitgehend ausschließen zu können. Ausschlaggebend sind die Adhäsions- und Kohäsionskräfte zwischen den Materialien. Es bilden sich je nach Material Van-der-Waals-Kräfte oder in polarisierten Werkstoffen wasserstoffbrückenähnliche Kräfte zwischen den Oberflächen. Am höchsten ist die Werkstoffhaftung bei ionischen Werkstoffen wie z. B. Kochsalz.

Berechnung der Reibungskraft

Mit Hilfe des Reibungskoeffizienten lässt sich die maximale Haft- bzw. die Gleitreibungskraft zwischen zwei Körpern berechnen.

Haftreibung:

F_{\mathrm {R,H} }\leq \mu _{\mathrm {H} }\cdot F_{\mathrm {N} }

maximale Haftreibung:

F_{\mathrm {R,max} }=\mu _{\mathrm {H} }\cdot F_{\mathrm {N} }

Gleitreibung:

F_{\mathrm {R,G} }=\mu _{\mathrm {G} }\cdot F_{\mathrm {N} }

Dabei ist $F_{\mathrm {R} }$ die Reibungskraft, $\mu _{\mathrm {H} }$ bzw. $\mu _{\mathrm {G} }$ der Reibungskoeffizient und $F_{\mathrm {N} }$ die Normalkraft (Kraft senkrecht zur Fläche). Der Reibungskoeffizient bestimmt also, wie groß die Reibungskraft im Verhältnis zur Normalkraft ist; eine höhere Reibungszahl bedeutet eine größere Reibungskraft.

Um beispielsweise einen Metallklotz zu schieben, muss man zunächst eine Kraft aufbringen, die höher als die Haftreibungskraft ist. Wenn der Klotz dann über den Untergrund gleitet, so reicht die kleinere Gleitreibungskraft. Weil die Reibkoeffizienten vom Untergrund (trocken, nass, …) abhängig sind, hängen im gleichen Maße auch die Reibkräfte davon ab.

Um die Haftung zu verändern, kann man auch die Normalkraft verändern, was sich wiederum aus der Formel erkennen lässt. Auf der Ebene entspricht die Normalkraft der Gewichtskraft, in Steilkurven die Komponente der Vektorsumme aus Gewichtskraft und Fliehkraft senkrecht zur Fahrbahn. Im Motorsport wird die Normalkraft durch Flügel (englisch Spoiler) erhöht, die den Fahrtwind zum Anpressen des Fahrzeugs an den Boden nutzen.

Beispiele

Die Reibungskoeffizienten aus Tabellen sind immer nur ungefähre Angaben. Die Reibung hängt von vielen unterschiedlichen Faktoren ab (Materialpaarung, Oberfläche, Schmierung, Temperatur, Feuchte, Verschleiß, Normalkraft etc.), so dass in einer Tabelle nicht die „richtigen“ Werte gefunden werden können.

Die genauesten Ergebnisse erhält man aus einem Versuch unter realen Bedingungen. Auch hier ist jedoch zu beachten, dass sich die Verhältnisse zwischen Versuch und realem Einsatz ändern können.

Es gilt immer:

\mu \leq \mu _{\mathrm {H} }

Haftreibung und Gleitreibung
(Richtwerte, trocken)[1]
Materialpaarung	Haftreibung	Gleitreibung
Stahl auf Stahl	0,2	0,1
Stahl auf Holz	0,5	0,4
Stahl auf Stein	0,8	0,7
Stein auf Holz	0,9	0,7
Leder auf Metall	0,6	0,4
Holz auf Holz	0,5	0,4
Stein auf Stein	1,0	0,9
Stahl auf Eis	0,03	0,01
Stahl auf Beton	0,35	0,20

Haftreibungszahlen

Haftreibungszahlen µ_H (Richtwerte)[2]
Materialpaarung		trocken	wenig fettig	geschmiert	mit Wasser
Bronze auf	Bronze	0,18		0,11
	Grauguss	0,56		0,73
	Stahl	0,19		0,18
Grauguss auf	Eiche				0,98
Grauguss auf	Grauguss		0,2	0,21
Eiche auf Eiche		0,58			0,71
Lederriemen auf	Eiche		0,49
Lederriemen auf	Grauguss	0,48	0,28	0,12	0,38
Messing auf Eiche		0,62		0,15
Stahl auf	Bronze	0,19
	Eiche			0,11	0,65
	Eis	0,027
	Grauguss	0,19
	Stahl	0,15	0,13
	Aluminium	0,19
Hanfseil auf Holz		0,5

Maximaler Kraftschlussbeiwert

Ein angetriebener oder gebremster Reifen hat gegenüber der Oberfläche, auf der er rollt, immer einen Schlupf. Dieser Schlupf ist bei kleinen übertragenen tangentialen Kräften so gering, dass er für viele Anwendungen vernachlässigt werden kann. Bei höherer Tangentialkraft nimmt der Schlupf zunächst schwach, dann immer stärker zu. Dies bedeutet, dass bei gegebenem Andruck eine maximale Tangentialkraft übertragen werden kann. Dies ähnelt dem Übergang von der Haftreibung zur Gleitreibung. Der Quotient zwischen der Tangentialkraft und der Normalkraft wird Kraftschlussbeiwert genannt. Sein Maximum gibt an, welche Kraft ein Reifen bei gegebener Normalkraft maximal als Antrieb, oder Bremskraft übertragen kann.

max. Kraftschlussbeiwerte µ_H (Richtwerte)[2]
Paarung	trocken	nass, sauber	nass, geschmiert	vereist
Luftreifen auf Ackerboden	0,45		0,2	<0,2
Luftreifen auf Erdweg	0,45		0,2	<0,2
Luftreifen auf Holzpflaster	0,55	0,3	0,2	<0,2
Luftreifen auf Kleinpflaster	0,55	0,3	0,2	<0,2
Luftreifen auf Kopfsteinpflaster	0,6	0,4	0,3	<0,2
Luftreifen auf Schotter, gewalzt	0,7	0,5	0,4	<0,2
Luftreifen auf Schotter, gewalzt, asphaltiert	0,6	0,4	0,3	<0,2
Greiferräder auf Ackerboden	0,5
Kettenfahrzeuge auf Ackerboden	0,8

Gleitreibungszahlen

Gleitreibungszahlen µ_G (Richtwerte)[2]
Materialpaarung	trocken	wenig fettig	geschmiert	mit Wasser
Bronze auf Bronze	0,20		0,06
Bronze auf Grauguss	0,21	0,08
Bronze auf Stahl	0,18	0,16	0,07
Grauguss auf Bronze	0,20	0,15	0,08
Grauguss auf Eiche	0,49	0,19		0,22
Grauguss auf Grauguss	0,28	0,15	0,08	0,31
Eiche auf Eiche	0,34		0,1	0,25
Lederriemen auf Eiche	0,27			0,29
Lederriemen auf Grauguss	0,56	0,27	0,12	0,36
Messing auf Eiche	0,60		0,44	0,24
Stahl auf Bronze	0,18	0,16	0,07
Stahl auf Eiche	0,5		0,08	0,26
Stahl auf Eis	0,014
Stahl auf Grauguss	0,18		0,01
Stahl auf Stahl	0,12		0,01
Stahl auf Messing	0,2
Stahl auf Weißmetall	0,2	0,1	0,04
blockiertes Autorad auf Pflaster	0,5			0,2

Geometrische Interpretation

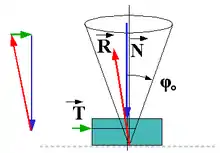
Abbildung 1: Resultierende Kraft innerhalb des Reibkegels

Man kann $\mu$ auch als Tangens des Reibungswinkels $\varphi$ betrachten. Dies ist der kleinste Winkel, bei dem ein Körper auf einer geneigten Ebene nach unten rutschen würde. Es gilt

\mu =\tan(\varphi )

.

Beispiel Auto: Der Tangens ist aus dem Alltag als Steigung von ansteigenden Straßen und Gefällen bekannt, die auf Verkehrsschildern angegeben wird (zum Beispiel: 12 % Steigung bedeuten, auf einer Länge von 100 m steigt die Strecke um 12 m). Bei einem Haftreibungskoeffizienten von Eins kann man also Steigungen von maximal 100 % (45°) überwinden. Real ist die Steigfähigkeit von Fahrzeugen meist durch die installierte Motorleistung und das Gesamtübersetzungsverhältnis der Getriebe begrenzt – Ausnahmen sind schlechte Straßenverhältnisse. Bei Glatteis oder schneebedeckter Straße wird die Haftreibungszahl sehr klein, so dass schon leichte Steigungen nicht überwunden werden können oder das Bremsen bergab nicht mehr möglich ist.

Reibkegel: Innerhalb des Reibkegels (Abbildung 1) sind Systeme auch bei Belastung stabil (z. B. Leiter auf Untergrund) und werden als selbsthemmend bezeichnet, außerhalb des Reibkegels reicht die Reibkraft nicht mehr aus, um das System in Ruhe zu halten, es tritt eine Bewegung auf. Relevante technische Systeme sind z. B. Schneckengetriebe, die in Abhängigkeit von Schraubensteigung, Materialpaarung und Schmierverhältnissen selbsthemmend sind oder nicht.

Grenzen

Erreichen die durch die auftretenden Kräfte verursachten Spannungen die Fließspannung, endet der Gültigkeitsbereich des coulombschen Modelles. An seine Stelle tritt das Reibfaktormodell.

Häufige Irrtümer

„µ ist immer kleiner als Eins“

Gelegentlich wird behauptet, dass $\mu \leq 1$ gelten müsse. $\mu =1$ bedeutet lediglich, dass Normal- und Reibungskraft gleich sind. Bei etlichen Materialpaarungen, beispielsweise mit Silikonkautschuk oder Acrylkautschuk beschichteten Oberflächen, ist der Reibkoeffizient wesentlich größer als Eins.

„Haftreibung ist Haftreibungskoeffizient mal Normalkraft“

Häufig wird für die Haftreibung die Formel

F_{\mathrm {R,H} }=\mu _{\mathrm {H} }\cdot F_{\mathrm {N} }

angegeben. Der so errechnete Wert bezeichnet jedoch nur den Grenzfall der maximal möglichen Schub- oder Zugkraft, die der Reibungskraft $F_{\mathrm {R} }$ entgegenwirkt und bei der noch der Stillstand des Objekts möglich ist. Wird diese überschritten, wirkt sofort die zumeist kleinere Gleitreibungskraft:

F_{\mathrm {R,G} }=\mu _{\mathrm {G} }\cdot F_{\mathrm {N} }

Augenscheinlich wird dies z. B. bei Lawinen oder Erdrutschen. Hier befinden sich die Massen nahe der Haftkraft. Kleine Erschütterungen lassen die Haftreibung örtlich überschreiten.

Literatur

Valentin L. Popov: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation. Springer-Verlag, Berlin u. a. 2009, ISBN 978-3-540-88836-9.

Quellen

Rainer Müller: Klassische Mechanik: vom Weitsprung zum Marsflug. Walter de Gruyter, 2009, S. 115 (eingeschränkte Vorschau in der Google-Buchsuche).
Horst Kuchling: Taschenbuch der Physik. VEB Fachbuchverlag, Leipzig 1986, ISBN 3-87144-097-3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[mechanik-1] Rainer Müller: Klassische Mechanik: vom Weitsprung zum Marsflug. Walter de Gruyter, 2009, S. 115 (eingeschränkte Vorschau in der Google-Buchsuche).

[Kuchling-2] Horst Kuchling: Taschenbuch der Physik. VEB Fachbuchverlag, Leipzig 1986, ISBN 3-87144-097-3.