Rad des Aristoteles

Als Rad des Aristoteles bzw. Rota Aristotelis wird ein mechanisches Paradoxon bezeichnet, das in den Quaestiones mechanicae beschrieben wird. Das Werk wird Aristoteles zugeschrieben, der tatsächliche Urheber ist allerdings nicht bekannt.

Problembeschreibung

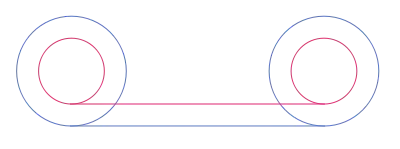
Nach einer vollständigen Umdrehung sind die Verbindungsstrecken zwischen den bodennähsten Punkten beider Räder gleich lang.

Betrachtet wird der Berührungspunkt eines Rades mit dem Boden. Bei einer vollständigen Umdrehung des Rades zeichnet dieser Punkt in Fahrtrichtung eine Strecke, deren Länge gleich dem Umfang des Rades ist. Wird an der gleichen Achse ein zweites Rad mit einem kleineren Durchmesser starr befestigt und hier ebenfalls der Punkt beobachtet, der dem Boden am nächsten ist, so legt dieser Punkt bei der Umdrehung die gleiche Strecke zurück. Der offensichtliche Widerspruch entsteht, wenn aus der Gleichheit der beiden Strecken gefolgert wird, dass beide Räder den gleichen Umfang haben.[1]

Lösung

Das große Sechseck hinterlässt beim „Abrollen“ eine kontinuierliche Spur, während der Pfad des kleineren Sechseckes Lücken aufweist.

Aus physikalischer Sicht entspricht der zurückgelegte Weg des betrachteten Punktes nur dann dem Radumfang, wenn eine echte Rollbewegung vorliegt. Dies ist für beide Räder aber nicht gleichzeitig möglich. Rollt das große Rad auf dem Boden ab, führt das kleinere Rad entlang der gedachten Linie zusätzlich eine gleitende Bewegung aus. Umgekehrt dreht das große Rad teilweise durch (Schlupf), wenn das kleinere Rad abrollt.[2]

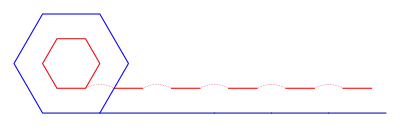
1638 stellte Galileo Galilei in seinem Werk Discorsi e dimostrazioni matematiche einen mathematischen Lösungsansatz für das Paradoxon vor. Dafür werden die beiden Räder zunächst als verschieden große Sechsecke angenommen. Beim Abrollen des großen Sechseckes erhält man wieder eine zusammenhängende Linie, deren Länge gleich dem Umfang dieses Sechsecks ist. Für die Strecke, die hierbei das kleine Sechseck hinterlässt, gilt dies ebenfalls; jedoch ist sie durch mehrere Lücken unterbrochen. Wird nun die Zahl der Ecken gedanklich bis ins Unendliche erhöht, sodass die Räder wieder kreisförmig sind, werden die unendlich vielen Lücken unendlich klein und die Strecke erscheint zusammenhängend. Lediglich die abgerollte Strecke des großen Rades ist ohne Unterbrechungen und damit tatsächlich so lang wie der Radumfang.[3]

Einzelnachweise

Thomas Nelson Winter: The Mechanical Problems in the Corpus of Aristotle (= Faculty Publications, Classics and Religious Studies Department. Paper 68). University of Nebraska-Lincoln, 2007, S. 26 ff. (PDF; 352 KB).
Stanley J. Farlow: Paradoxes in Mathematics. Dover Publications, Mineola (New York) 2014, ISBN 978-0-486-49716-7, S. 92 ff.
Thomas Sonar: 3000 Jahre Analysis: Geschichte – Kulturen – Menschen. 2. Auflage. Springer Verlag, Berlin 2016, ISBN 978-3-662-48917-8, S. 203 f.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Thomas Nelson Winter: The Mechanical Problems in the Corpus of Aristotle (= Faculty Publications, Classics and Religious Studies Department. Paper 68). University of Nebraska-Lincoln, 2007, S. 26 ff. (PDF; 352 KB).

[2] Stanley J. Farlow: Paradoxes in Mathematics. Dover Publications, Mineola (New York) 2014, ISBN 978-0-486-49716-7, S. 92 ff.

[3] Thomas Sonar: 3000 Jahre Analysis: Geschichte – Kulturen – Menschen. 2. Auflage. Springer Verlag, Berlin 2016, ISBN 978-3-662-48917-8, S. 203 f.