QuickHull
QuickHull ist ein Algorithmus zur Berechnung der konvexen Hülle einer beliebigen endlichen Menge von Punkten im zwei- oder dreidimensionalen Raum. Die konvexe Hülle einer Menge von Punkten wird beschrieben durch einen geschlossenen Polygonzug, der die Verbindung aller Extremalpunkte der Menge darstellt, und somit alle Punkte der Menge einschließt. Eine häufig verwendete intuitive Erklärung dieser Hülle ist ein Gummiband, welches sich um die Punktemenge spannt. Dieses bildet, wenn es straff auf allen äußeren Punkten aufliegt, die konvexe Hülle der Punktemenge.
Namensgebung und Entstehung
Der Name QuickHull leitet sich aus der Ähnlichkeit zu Quicksort ab, einem Algorithmus zum Sortieren beliebiger Mengen. Er findet zum ersten Mal Erwähnung im Buch Computational geometry von Franco Preparata und Michael Shamos,[1] in dem die beiden Autoren den hier beschriebenen Algorithmus vorstellen, der die Ideen anderer Autoren aufgreift.[2][3][4]
Grundidee
Die algorithmische Idee zu QuickHull kommt aus dem Prinzip „Teile und Herrsche“, das in der Informatik häufig zum Einsatz kommt. Es beschreibt die Vorgehensweise, das Problem in mehrere kleine Probleme zu unterteilen und diese dann durch Anwendung des gleichen Algorithmus rekursiv zu lösen. In diesem Zusammenhang wird oft versucht, die Teilung so geschickt zu wählen, dass durch diese bereits eine große Anzahl von ungültigen Lösungsmengen herausfallen. Durch diese Art des Aufbaus können Algorithmen, die nach diesem Prinzip entworfen worden, häufig einfach und gut lesbar implementiert werden, da sie eine verständliche rekursive Struktur besitzen.
Pseudocode
Bezeichnungen: S ist die Menge der gegebenen Punkte, Sk ist die Menge der Punkte auf einer Seite der Geraden durch die Punkte P und Q.[5]
Funktion QuickHull(S)
{
// Bestimmt die konvexe Hülle der Menge S
Convex Hull := {}
A := Punkt ganz links
B := Punkt ganz rechts
Füge die Punkte A und B der konvexen Hülle hinzu
// Die Gerade AB teilt die verbleibenden n - 2 Punkte in die Teilmengen S1 und S2
S1 := Menge der Punkte in S, die auf der rechten Seite von AB sind
S2 := Menge der Punkte in S, die auf der linken Seite von AB sind
FindHull(S1, A, B)
FindHull(S2, B, A)
Ausgabe: Convex Hull
}
Funktion FindHull(Sk, P, Q)
{
// Bestimmt die Punkte auf der konvexen Hülle der Menge Sk, die auf der rechten Seite der Geraden PQ sind
Wenn Sk keine Punkte enthält dann
Ausgabe: Convex Hull
C := Der Punkt in Sk, der den größten Abstand von der Geraden PQ hat
Füge den Punkt C in die konvexe Hülle zwischen den Punkten P und Q ein
// Die drei Punkte P, Q und C teilen die verbliebenen Punkte von Sk in die Teilmengen S0, S1 und S2
S0 := Die Punkte innerhalb des Dreiecks PCQ
S1 := Die Punkte auf der rechten Seite der Geraden PC
S2 := Die Punkte auf der rechten Seite der Geraden CQ
FindHull(S1, P, C)
FindHull(S2, C, Q)
Ausgabe: Convex Hull
}
Beispiel

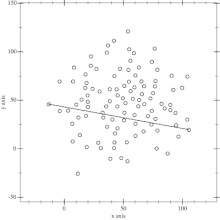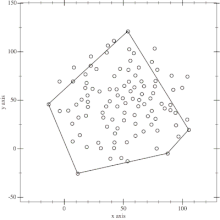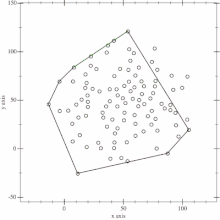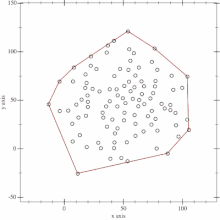
Der Algorithmus operiert auf einer beliebigen endlichen Menge von Punkten. Es bestehen keinerlei besondere Anforderungen an die Anordnung oder Anzahl der Punkte. Eine symmetrische Anordnung der Punkte besitzt jedoch eine höhere Wahrscheinlichkeit die Best Case (bester Fall) Laufzeitschranke von zu verlassen und deutlich langsamer zu sein.

Zur Bestimmung der ersten Aufteilung der Menge werden die beiden Extremalpunkte der X-Achse gesucht. Also diejenigen Punkte, welche am weitesten links und am weitesten rechts liegen. Diese Punkte können bereits dem Polygonzug der Konvexen Hülle hinzugefügt werden, da sie als Extrempunkte garantiert Bestandteil derselben sind.
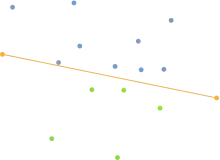
Die beiden gefundenen Punkte bilden eine Gerade, welche die Punktmenge in zwei Bereiche teilt. Alle Punkte links von der Geraden repräsentieren eine Menge und alle Punkte rechts von der Gerade die andere. Rechts und links ergeben sich in diesem Zusammenhang aus dem Winkel zwischen dem Richtungsvektor der Trennungsgeraden und dem Vektor definiert durch den Anfangspunkt der Geraden und den zu überprüfenden Punkt. Ist dieser Winkel kleiner als 180°, dann wird der Punkt als rechts von der Geraden betrachtet, bei Winkeln größer 180° als links von ihr.
Die beiden durch diese Gerade getrennten Punktmengen werden nun rekursiv mit dem QuickHull Algorithmus weiter verarbeitet. In diesem Beispiel wird lediglich der linke Teil der Punktemenge weiter betrachtet. Alle gemachten Aussagen treffen äquivalent auch auf den rechten Teil zu.
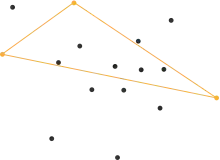
Innerhalb der betrachteten Punktmenge wird jener Punkt bestimmt, der die maximale Distanz von der Geraden besitzt. Dieser ist offensichtlich ebenfalls ein Bestandteil des gesuchten Polygonzugs. Zusammen mit dem Start- und Endpunkt der Geraden entsteht ein Dreieck.
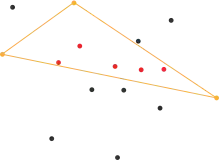
Das Dreieck setzt sich zusammen aus drei Punkten, von denen alle Bestandteil des Konvexen-Hülle-Polygons sind. Aus diesem Grund können alle Punkte im Inneren dieses Dreiecks nicht Bestandteil dieses Polygons sein, da sie ja bereits in seinem Inneren liegen. Alle Punkte innerhalb dieses Dreiecks können also bei weiteren rekursiven Aufrufen des Algorithmus ignoriert werden.
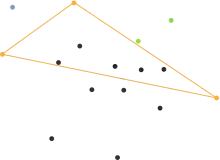
Die sich als Seiten des Dreiecks ergebenden Geraden werden nun als erneute Trenngeraden der Punktemenge betrachtet. Alle Punkte links von dem Dreieck repräsentieren eine Menge, alle Punkte rechts von dem Dreieck die andere.
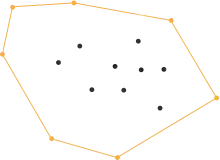
Diese rekursive Aufteilung und Bestimmung weiterer Punkte wird so lange wiederholt, bis nur noch der Start- und Endpunkt der Trenngeraden Bestandteil der zu betrachtenden Punktmenge sind, denn in diesem Fall ist klar, dass diese Gerade ein Segment des gesuchten Polygonzugs darstellt.
Einzelnachweise
- Franco P. Preparata, Michael Ian Shamos: Computational Geometry. An Introduction. 1. Auflage. Springer-Verlag, 1985, ISBN 0-387-96131-3.
- William F. Eddy: A New convex Hull Algorithm for Planar Sets. In: ACM Transactions on Mathematical Software. 3, 1977, S. 393–403.
- Alex Bykat: Convex Hull of a Finite Set of Points in Two Dimensions. In: Information Processing Letters. 7, 1978, S. 296–298.
- P. J. Green, B.W. Silverman: Constructing the Convex Hull of a Set of Points in the Plane. In: Computer Journal. 22, 1979, S. 262–266.
- OpenGenus IQ: Quick Hull Algorithm to find Convex Hull